Extraction of an Explanatory Graph to Interpret a CNN

1   Introduction

In this paper, we investigate the disentanglement of intermediate-layer feature representations of a CNN pre-trained for object classification. We notice that each filter in a CNN usually encodes mixed features of object parts and textural patterns. Therefore, in this paper, given a CNN, we propose to learn an explanatory graph without any part annotations. The explanatory graph automatically reveals how object-part features are organized in the CNN. The explanatory graph

1. disentangles features of object parts from mixed features in intermediate-layers of a CNN;

2. encodes which object parts are usually co-activated and keep the stable spatial relationship.

As Fig. 1 shows, the explanatory graph encodes the compositional hierarchy of object parts encoded inside conv-layers of the CNN, as follows.

• The explanatory graph consists of multiple layers. Each layer of the graph corresponds to a conv-layer of the CNN and contains thousands of nodes.
• Each node represents an object part that is encoded in a filter of a conv-layer. A filter in a conv-layer is usually activated by multiple parts and textural patterns. As Fig. 1 shows, a filter’s feature map¹1. The output of a conv-layer is called the feature map of a conv-layer. Each channel of this feature map is produced by a filter, so we call a channel the feature map of a filter. may be activated by both the head and the neck of a horse.
• Given the feature map of a filter, a graph node can identify neural activations in the feature map, which correspond to a specific object part. Theoretically, a CNN with ReLU layers can be considered to encode high-order piecewise linear representations. An object part corresponding to a node is encoded inside a specific feature space divided by the piecewise partitions. Multiple nodes are learned for each filter, i.e., neural activations in its feature map are divided and explained as different multiple parts.
• A graph edge connects two nodes in adjacent layers. The two connected nodes represent two object parts, which usually appear simultaneously in an image and keep a stable spatial relationship among different images. For example, the ear part and the face part of a horse usually co-appear on different images with similar spatial relationships.

Constructing the explanatory graph is a process of mining object parts from intermediate conv-layers. Nodes in the explanatory graph represent all candidate parts learned from the entire set of training images by the CNN. Consequently, in the inference process, given an input image, the explanatory graph automatically selects a small ratio of nodes. These chosen nodes identify neural activations in intermediate-layer feature maps, which correspond to specific object parts. Given different images, the explanatory graph selects different sets of nodes for explanation. Moreover, since the same part may appear at various locations, given different images, the same node may identify neural activations at different positions as the target part.

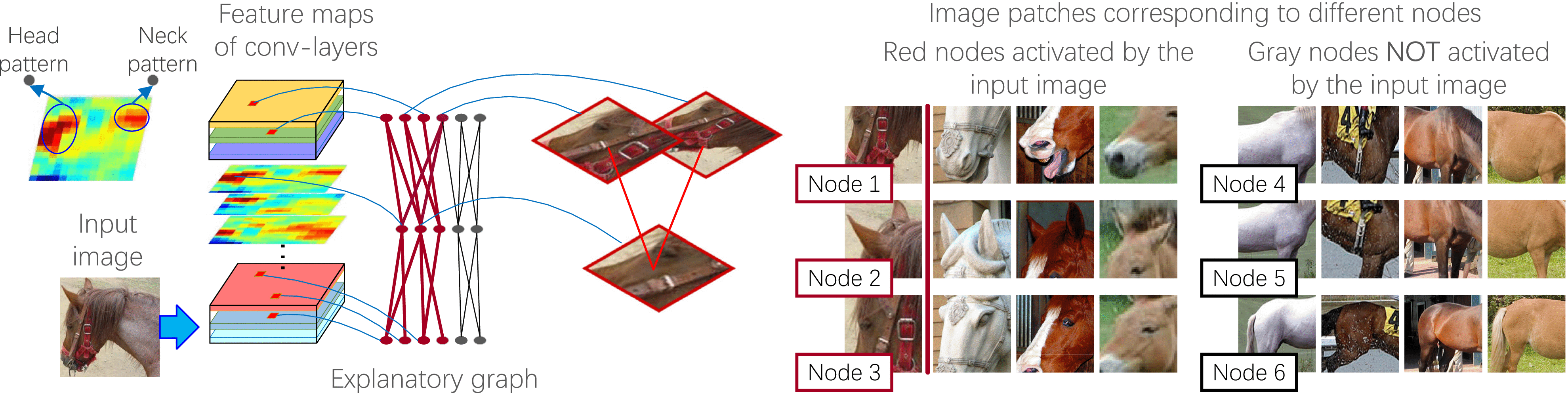
Fig. 1. An explanatory graph represents the compositional hierarchy of object parts encoded in conv-layers of a CNN. Each filter in a pre-trained CNN may be activated by different object parts. Our method disentangles object parts from each filter in an unsupervised manner.

The explanatory graph mainly takes two advantages, i.e., the disentanglement and the transferability, as follows.

Disentangling object parts from a single filter is the core technique of building an explanatory graph. In this study, we develop a simple yet effective method to automatically disentangle different object parts from a single filter without using any annotations of object parts, which presents considerable challenges for state-of-the-art algorithms. In this way, the explanatory graph exclusively localizes neural activations of object parts in the feature map, and ignores noisy activations and activations of textural patterns.

More specifically, for each input image, the explanatory graph (i) infers which parts (nodes) are responsible for the feature map of a filter and (ii) localizes these parts.

Graph Nodes With High Transferability . The explanatory graph contains off-the-shelf features of object parts in a compositional hierarchy, like a dictionary. Thus, the explanatory graph enables us to accurately transfer such object-part features to other tasks. Since all filters in the CNN are learned to encode common features shared by numerous training images, each graph node can be regarded as a transferable detector for common parts among different images.

To demonstrate the above advantages, we learn different explanatory graphs for various CNNs (e.g., the VGG-16, residual networks, and the encoder of a VAE-GAN) and analyze the explanatory graphs from various perspectives as follows.

Visualization & Reconstruction . We visualize object parts encoded by graph nodes using the following two approaches. First, for each graph node, we draw image regions corresponding to the node’s part localizations on different input images. Second, we learn another neural network, which uses activation states of graph nodes to reconstruct the input image.

Evaluation of Part Interpretability of Graph Nodes . Given an explanatory graph, we propose a new metric to quantitatively evaluate whether a node consistently represents the same part in different images.

Examination of Location Instability of Graph Nodes . Besides the part interpretability, we also use a new metric, namely location instability, to measure the semantic clarity of each graph node. It is assumed that if a graph node consistently represents the same object part, then the distances between the inferred part and some ground-truth landmarks of the object should not change a lot through different images. Thus, the evaluation metric uses the deviation of such relative distances over images to measure the instability of the part representation.

Testing Transferability . The transferability of graph nodes is tested in the scenario of few-shot part localization. We associate certain graph nodes with explicit part names based on feature maps of very few images, in order to localize the target part. The superior localization performance proves the good transferability of graph nodes.

Contributions of this paper are summarized as follows.

• In this paper, we, for the first time, propose a simple yet effective method to extract and summarize object parts encoded inside intermediate conv-layers of a CNN and organize them using an explanatory graph. Experiments show that each graph node consistently represented the same object part in different input images.
• The proposed method can be used to learn explanatory graphs for various CNNs, e.g., VGGs, residual networks, and the encoder of a VAE-GAN.
• Graph nodes have good transferability, especially in the task of few-shot part localization. Although our graph nodes were learned without part annotations, our transfer-learning-based part localization still outperformed approaches using part annotations to learn part representations.

A preliminary version of this paper appeared in ^[43].

2   Related work

2.1 Semantics in the CNN

The interpretability of neural networks receives increasing attention in recent years ^[51]. Different methods have been developed to explore visual concepts encoded inside a CNN.

Visualization & Interpretability of CNN Filters . Visualization of filters in a CNN is the most direct way of diagnosing representations of a CNN. Dosovitskiy et al. ^[6] proposed up-convolutional nets to invert feature maps of conv-layers to input images. Gradient-based visualization ^{[19],[21],[22],[31]} showed the appearance that maximized a network output, the activation score of a specific filter, or certain neural activations in a feature map. Furthermore, Bau et al. ^[3] defined and analyzed the interpretability of each filter. In recent years, ^[23] provided a reliable tool to visualize filters in different conv-layers of a CNN.

^[3] selectively analyzed the semantics among the highest 0.5 percent activations of each filter. In contrast, our method provides a solution to explaining both strong and relatively weak activations from each filter, instead of exclusively extracting significant neural activations.

Active Network Diagnosis . Going beyond “passive” visualization, some methods “actively” diagnose a pre-trained CNN to obtain insight understanding of CNN representations. Many statistical methods ^[1],[35] have been proposed to analyze CNN features. ^[35] explored semantic meanings of convolutional filters. ^[1],[17] computed feature distributions of different categories.

The model bias and dataset bias are typical problems in deep learning, which has been illustrated in recent studies of ^{[14],[20],[24]}. Zhang et al. ^[47] has proposed a method to discover biased representations due to dataset bias. The CNN usually uses unreliable contexts for classification. For example, a CNN may extract features from hairs as a context to identify the smiling attribute.

Therefore, in order to ensure the correctness of feature representations, network-attack methods ^{[12],[34],[35]} diagnosed network representations by computing adversarial samples for a CNN. In particular, influence functions ^[12] were proposed to compute adversarial samples, create training samples to attack the learning of CNNs, fix the training set, and further debug a CNN. ^[13] discovered blind spots of CNN representations in a weakly-supervised manner. In comparison, our method disentangles features of object parts from a pre-trained CNN and builds an explanatory graph to reveal object parts encoded inside the CNN. It is because just like And-Or graphs ^{[39],[40],[41],} our explanatory graph naturally represents the local, bottom-up, and top-down information to construct a hierarchical object representation.

Diagnosis of Network Predictions . Some previous studies aimed to explain the reason for each network prediction. Methods of ^[7],[27] propagated gradients of feature maps w.r.t. the CNN loss back to the image, in order to estimate the image regions that directly contribute the network output. The LIME ^[24], the SHAP ^[18], and ^[4],[42] extracted input units that were closely related to a specific prediction.

Pattern Retrieval . Some studies retrieve specific activation units with specific meanings from intermediate-layer feature maps. Like middle-level feature extraction ^[33], pattern retrieval mainly learns mid-level representations of CNN features. Zhou et al. ^[52],[53] selected activation units from feature maps to describe scenes. In particular, ^[52] accurately computed the image-resolution receptive field of neural activations in a feature map. Theoretically, the actual receptive field of a neural activation is smaller than that computed using the filter size. Simon et al. discovered objects from feature maps of unlabeled images ^[29], and selected a filter to describe each part in a supervised fashion ^[30]. However, most methods simply assumed that each filter mainly encoded a single visual concept, and ignored the case that a filter in high conv-layers encoded a mixture of object parts and textural patterns. ^{[44],[45],[46]} extracted certain neural activation units from a filter’s feature map to describe an object part in a weakly-supervised manner (i.e., learning from active question answering and human interactions).

Fig. 2. Schematic illustration of the explanatory graph. The explanatory graph encodes spatial and co-activation relationships between object parts in the explanatory graph. Nodes in high layers help localize nodes in low layers. From another perspective, we can regard low-layer nodes represent compositional parts of high-layer nodes.

In this study, the explanatory graph disentangles features of different object parts from the CNN without part annotations. Compared to raw feature maps, graph nodes are well disentangled and more interpretable.

CNN Semanticization . Compared to the diagnosis of CNN representations and the pattern retrieval, semanticization of CNN representations is closer to the spirit of building interpretable representations.

Hu et al. ^[11] designed logic rules for network outputs, and used these rules to regularize neural networks and learn meaningful representations. ^[3],[52] extracted visual semantics from intermediate layers of a CNN. ^[37] distilled representations of a neural network into an additive model to explain the network. ^[53] also used additive structures, i.e., the global average pooling layer to explain neural networks. ^[50] used a tree structure to approximate the rationale of the CNN prediction on each specific sample. Capsule nets ^[26] and interpretable CNNs ^[49] used specific network structures and loss functions, respectively, to make the network automatically encode interpretable features in intermediate layers.

In comparison, we aim to explore the compositional hierarchy of object parts encoded inside conv-layers of a CNN. The explanatory graph boosts the transferability of CNN features to other part-based tasks.

2.2 Weakly-Supervised Knowledge Transferring

Knowledge transferring has been widely used in deep learning. Typical research includes end-to-end fine-tuning and transferring CNN representations between different datasets ^[8]. In contrast, a transparent representation of the explanatory graph will create a new possibility of transferring object-part features to other applications. Experiments have demonstrated the superior transferability of graph nodes in few-shot part localization.

3   Algorithm

A single filter is usually activated by different parts of the object (see Fig. 2). Let us assume that given an input image, a filter is activated at $N$ positions, i.e., there are $N$ activation peaks on the filter’s feature map. Some peaks represent common parts of the object. Other activation peaks may correspond to background noises or textural patterns.

Our goal is to disentangle activation peaks corresponding to object parts from a filter’s feature map. I.e., we select certain neural activations, which represent specific object parts. We propose an explanatory graph for the disentanglement. Each activation peak of a filter corresponding to an object part is represented as a graph node. Let an activation peak represent a specific object part. Then, it is assumed that the CNN usually contains other filters to represent neighboring parts of the target part. I.e., some activation peaks of other filters must keep stable spatial relationships with the target part. Such spatial relationships are encoded in edges of the explanatory graph, which connect each node in a layer to some nodes in the neighboring upper layer.

Object parts are mined layer by layer. Given object parts mined from the upper layer, we extract activation peaks that keep stable spatial relationships with specific upper-layer parts through different images, as parts in the current layer.

Nodes in high layers usually represent large-scale object parts, while nodes in low layers mainly describe small and relatively simple shapes, which are usually compositions of high-layer parts. Nodes in high layers are usually discriminative, and the explanatory graph uses high-layer nodes to filter out noisy activations. Nodes in low layers are disentangled based on their spatial relationship with high-layer nodes.

3.1 Explanatory Graph

Before the introduction of technical details of the algorithm, we first give a brief overview of the explanatory graph.

We are given a CNN, which is learned using a set of training samples ${\mathbf I}$. We construct an explanatory graph $G$ based on this CNN and all training samples in ${\mathbf I}$. As Fig. 4 illustrates, $G$ contains several layers, each corresponding to a single conv-layer in the CNN. Each layer of the explanatory graph is composed of hundreds/thousands of nodes, which represent object parts encoded in this conv-layer. Each node is linked with some graph nodes in the upper layer. The linkage/edge indicates that object parts of the two linked nodes usually co-appear in the image with stable spatial relationship. In this way, an explanatory graph can be considered as a dictionary of object parts, which are extracted from various images.

In the training phase, each node in $G$ is supposed to disentangle a part from a conv-layer’s feature maps. In inference phase, given feature maps of an input image $I$, the explanatory graph $G$ uses its nodes to localize neural activations corresponding to different parts.

3.2 Top-Down Iterative Learning of the Explanatory Graph

Given all training images ${\mathbf I}$, we expect that (i) all nodes in the explanatory graph can be well fitted to feature maps of all images, and (ii) nodes in the lower layer always keep consistent spatial relationships with nodes in the upper layer given each input images. Therefore, the learning of an explanatory graph is conducted in a top-down manner as follows.

The learning of an explanatory graph is conducted layer by layer. We first disentangle parts from the top conv-layer of the CNN and construct the top layer of the explanatory graph. Then, we conduct position inferences for all nodes in the top layer (the inference process will be introduced in Section 3.3). We use inference results to help disentangle parts from the neighboring lower conv-layer. In this way, the lower layer of the explanatory graph is constructed using inference results of the neighboring upper layer.

Fig. 3. Schematic illustration of related nodes $V$ and $V^{\prime }$. The related nodes keep similar spatial relationships among different images. Circle centers represent the prior part positions, e.g., $\mu _{V}$ and $\mu _{V^{\prime }}$. Red arrows denote relative displacements between the inferred positions and prior positions, e.g., ${\mathbf p}_{V}-\mu _{V}$. In particular, the middle sub-figure illustrates different variables in a one-dimensional space for simplicity.

Construction of the $L$th ²2. Note that our method is not limited to using consecutive conv-layers to learn the explanatory graph. People can select inconsecutive conv-layers. Without loss of generality, the $L$th ranked layer among all conv-layers, which are selected from the CNN, is termed as the $L$th conv-layer for simplicity. Layer . In the following paragraphs, we will introduce how to recursively learn the $L$th layer of the explanatory graph given the $(L+1)$-th layer.

Our method disentangles the $d$th filter of the $L$th conv-layer into $N_{L,d}$ parts. These parts are modeled as a set of $N_{L,d}$ nodes in the $L$th layer of $G$, denoted by $\Omega _{L,d}$. $\Omega _{L}=\cup _{d}\Omega _{L,d}$ denotes the entire node set for the $L$th layer. In following paragraphs, we can simply omit the subscript $L$ without ambiguity. ${\boldsymbol{\theta }}$ represents parameters of nodes in the $L$th layer, which mainly encode spatial relationships between these nodes and nodes in the $(L+1)$-th layer. Table 1 summarizes the notation used in this paper.

Given an input image $I\in {\mathbf I}$, the $L$th conv-layer of the CNN generates a feature map¹, denoted by ${\mathbf X}^{I}$. Then, for each node $V\in \Omega _{d}$, the explanatory graph infers whether or not the part indicated by $V$ appears in the $d$th channel¹ of ${\mathbf X}^{I}$, as well as its part location (if the part appears).

For each node $V$ in the $L$th layer, our method learns the following two terms: (i) the parameter $\mu _{V}\in {\boldsymbol{\theta }}$ and (ii) a set of nodes ${E}_{V}\in {\boldsymbol{\theta }}$ in the upper layer that are connected to $V$. $\mu _{V}\in {\boldsymbol{\theta }}$ denotes the prior location of $V$. Thus, for each node $V^{\prime }\in {E}_{V}$, $\mu _{V}-\mu _{V^{\prime }}$ corresponds the prior displacement between $V$ and node $V^{\prime }$ in the upper layer. The explanatory graph uses the displacement $\mu _{V}-\mu _{V^{\prime }}$ to model the spatial relationships between nodes.

Just like an EM algorithm, we use the current explanatory graph to fit feature maps of training images. Then, we use matching results as feedback to modify the prior location $\mu _{V}$ and edges ${E}_{V}$ of each node $V$ in the $L$th layer, in order to make the explanatory graph better fit the feature maps. We repeat this process iteratively to obtain the optimal prior location and edges for $V$.

In other words, our method automatically extracts pairs of related nodes and learns the optimal spatial relationships between them during the iterative learning process, which best fit feature maps of training images.

Therefore, the objective function of learning the $L$th layer is formulated as $$\begin{equation*} \arg \mathop{\!\max }_{{\boldsymbol{\theta }}}{\prod }_{I\in {\mathbf I}}P({\mathbf X}^{I}|{\mathbf R}^{I},{\boldsymbol{\theta }}). \tag{1} \end{equation*}$$ Let us focus on the feature map ${\mathbf X}^{I}$ of image $I$. Without ambiguity, we ignore the superscript $I$ to simplify notations in following paragraphs. We can regard ${\mathbf X}$ as a distribution of “neural activation entities.” The neural response of each unit $x\in {\mathbf X}$ can be considered as the number of “activation entities.” In other words, each neural activation unit $x$ in the feature map ${\mathbf X}$ is identified by its spatial position ${\mathbf p}_{x}$³ and its channel number $d_{x}$ (i.e., an activation unit of the $d_{x}$-th filter). We use $F(x)=\beta \cdot \max \lbrace f_{x},0\rbrace$ to measure the number of activation entities at the location ${\mathbf p}_{x}$, where $f_{x}$ is the normalized activation value of $x$; $\beta$ is a constant. We use ${\mathbf R}^{I}$ to represent position inference results of all nodes in the upper conv-layer (i.e., the $L+1$-th conv-layer).

Just like a Gaussian mixture model, all nodes in $\Omega _{d}$ comprise a mixture model, which explains the distribution of activation entities on the $d$th channel of ${\mathbf X}$. $$\begin{align*} P({\mathbf X}|{\mathbf R},{\boldsymbol{\theta }})&={\prod }_{x\in {\mathbf X}}P({\mathbf p}_{x}|{\mathbf R},{\boldsymbol{\theta }})^{F(x)}\\ &={\prod }_{x\in {\mathbf X}}\Bigg \lbrace \sum \limits _{V\in \Omega _{d}\cup \lbrace V_{\mathrm {none}}\rbrace }\!\!\!\!\!\!\!\!\!P(V)P({\mathbf p}_{x}|V,{\mathbf R},{\boldsymbol{\theta }})\!\Bigg \rbrace _{d=d_{x}}^{F(x)}\!,\tag{2} \end{align*}$$ where each node $V\in \Omega _{d}$ is treated as a hidden variable or an alternative component in the mixture model to describe activation entities. $P(V)=\frac{1}{N_{d}+1}$ is a constant prior probability. $P({\mathbf p}_{x}|V,{\mathbf R},{\boldsymbol{\theta }})$ measures the compatibility of using node $V$ to describe an activation entity at ${\mathbf p}_{x}$. In particular, we add a dummy node $V_{\mathrm {none}}$ to the mixture model for noisy activations, in order to explain neural activations unrelated to object parts, e.g., those of noises and textural patterns. The compatibility between $V$ and ${\mathbf p}_{x}$ is based on spatial relationship between $V$ and its connected nodes in $G$, which is approximated as $$\begin{align*} \!\!\!\!P({\mathbf p}_{x}|V,{\mathbf R},{\boldsymbol{\theta }})\!=\!\left\lbrace \!\begin{array}{ll}\gamma \prod \limits _{V^{\prime }\in {E}_{V}}P({\mathbf p}_{x}|{\mathbf p}_{V^{\prime }},{\boldsymbol{\theta }})^{\lambda }&V \in \!\Omega _{d_{x}}\\ \gamma \tau,&V=V_{\mathrm {none}}\\ \end{array}\right.\tag{3} \end{align*}$$ $$\begin{align*} P({\mathbf p}_{x}|{\mathbf p}_{V^{\prime }},{\boldsymbol{\theta }})\!=\!{\mathbf{\mathcal N}}({\mathbf p}_{x}|\mu _{V^{\prime }\!\rightarrow \!V},\sigma _{V^{\prime }}^2). \tag{4} \end{align*}$$ In the above equations, $V$ has $M$ related nodes in the upper layer. The set of nodes ${E}_{V}\in {\boldsymbol{\theta }}$ connected to $V$ would be determined during the learning process. The overall compatibility $P({\mathbf p}_{x}|V,{\mathbf R},{\boldsymbol{\theta }})$ is divided into the spatial compatibility between node $V$ and each related node $V^{\prime }$, $P({\mathbf p}_{x}|{\mathbf p}_{V^{\prime }},{\boldsymbol{\theta }})$. $\forall V^{\prime }\in {E}_{V}$, ${\mathbf p}_{V^{\prime }}\!\in \!{\mathbf R}$ denotes the position inference result of $V^{\prime }$, which have been given. $\lambda =\frac{1}{M}$ is a constant for normalization. $\gamma$ is a constant, which roughly ensures $\int P({\mathbf p}_{x}|V,{\mathbf R},{\boldsymbol{\theta }}){\mathbf d}{{\mathbf p}_{x}}=1$ and can be eliminated during the learning process.

As Fig. 3 shows, an intuitive idea is that the relative displacement between $V$ and $V^{\prime }$ should not change a lot among different images. Then, ${\mathbf p}_{x}-{\mathbf p}_{V^{\prime }}$ will approximate to the prior displacement $\mu _{V}-\mu _{V^{\prime }}$, if node $V$ can well fit the activation at ${\mathbf p}_{x}$. Given ${E}_{V}$, we assume the spatial relationship between $V$ and $V^{\prime }$ follows a Gaussian distribution in Eq. (4), where we define $\mu _{V^{\prime }\rightarrow V}=\mu _{V}-\mu _{V^{\prime }}+{\mathbf p}_{V^{\prime }}$ as the prior localization of $V$ given $V^{\prime }$. The variation $\sigma _{V^{\prime }}^2$ can be estimated from data.⁴

Algorithm 1.   Learning Sub-Graph in the $L$th Layer

The explanatory graph is learned in a top-down manner, and the learning process is summarized in Algorithm 1. Our method first learns nodes in the top-layer of $G$, and then learns for the neighboring lower layer. For the sub-graph in the $L$th layer, our method recursively estimates $\mu _{V}$ and ${E}_{V}$ for nodes in the sub-graph.

The special case is the node in the top conv-layer. For each node $V$ in the top conv-layer, we simply define ${E}_{V}\!=\!\lbrace V_{\mathrm {dummy}}\rbrace$, $\mu _{V_{\mathrm {dummy}}}={\mathbf p}_{V_{\mathrm {dummy}}}={\mathbf 0}$, where $V_{\mathrm {dummy}}$ is a node in the dummy layer above the top conv-layer. Based on Eqs. (3) and (4), we obtain $P({\mathbf p}_{x}|V,{\mathbf R},{\boldsymbol{\theta }})={\mathbf{\mathcal N}}({\mathbf p}_{x}|\mu _{V},\sigma _{V}^2)$.

3.3 Part Localization

Given feature maps of an input image, we can assign nodes with different activations peaks on feature maps, in order to infer object parts represented by these neural activations. The explanatory graph simply assigns node $V\in \Omega _{d}$ with the unit $\hat{x}={\arg \!\max }_{x\in {\mathbf X}:d_{x}=d}S_{V\rightarrow x}^{I}$ on the feature map as the inference of $V$. $S_{V\rightarrow x}^{I}\!=\!F(x)P({\mathbf p}_{x}|V,{\mathbf R},{\boldsymbol{\theta }})$ denotes the score of assigning $V$ to $x$. Accordingly, ${\mathbf p}_{V^{\prime }}={\mathbf p}_{\hat{x}}$ represents the inferred location of $V$. In particular, in Eqn. (1), we define ${\mathbf R}=\lbrace {\mathbf p}_{V^{\prime }}\rbrace _{V^{\prime }\in \Omega _{L+1}}$.

4   Experiments

In this section, we conducted several experiments to demonstrate the effectiveness, board applicability, and the high accuracy of our method. We learned explanatory graphs to interpret four types of CNNs, i.e., the VGG-16 ^[32], the 50-layer and 152-layer Residual Networks ^[10], and the encoder of the VAE-GAN ^[15]. These CNNs learned using a total of 37 animal categories in three datasets, which included the ILSVRC 2013 DET Animal-Part dataset ^[44], the CUB200-2011 dataset ^[38], and the VOC Part dataset ^[5]. As discussed in ^[5],[44], animals usually contain non-rigid parts, which presents a key challenge for part localization. Thus, we selected animal categories in the three datasets for testing.

We designed three experiments to evaluate the explanatory graph from different perspectives. In the first experiment, we visualized object parts corresponding to nodes in the explanatory graph. The second experiment was designed to evaluate the interpretability of nodes, i.e., checking whether or not a node consistently represents the same object part among different images. We compared our nodes with three types of middle-level features and network features. In the third experiment, we used our graph nodes for the task of few-shot part localization, in order to test the transferability of nodes. We learned an And-Or graph (AOG) with very few part annotations, which associated the well learned nodes with explicit part names. We used the AOG to conduct part localization and compared its performance with fourteen baselines.

4.1 Implementation Details

Fig. 4. A four-layer explanatory graph. For clarity, we put all nodes of different filters in the same conv-layer on the same plane and only show 1 percent of the nodes with 10 percent of their edges from two perspectives.

Fig. 5. Image patches corresponding to different nodes in explanatory graphs. We visualized nodes in explanatory graphs that were learned for two types of CNNs, i.e., CNNs learned for a single category and CNNs for multiple categories. (1) The top nine layers visualized nodes corresponding to CNNs, each learned for a single category. We used two methods to infer the image patch for each node. In top nine rows, part location was inferred as $\hat{x}={\arg \!\max }_{x\in {\mathbf X}:d_{x}=d}S_{V\rightarrow x}^{I}$. In following three rows, parts were localized via $\hat{x}={\arg \!\max }_{x\in {\mathbf X}:d_{x}=d}|f_{x}\cdot \frac{\partial y}{\partial f_{x}}|$. (2) The bottom four layers visualized image patches of graph nodes, when the CNN was learned to classify multiple categories. In this case, each node usually encoded parts shared by different categories. Texts before each group of image patches indicate their corresponding categories. Part location was inferred as $\hat{x}={\arg \!\max }_{x\in {\mathbf X}:d_{x}=d}S_{V\rightarrow x}^{I}$. Please read texts for detailed explanations.

Fig. 6. Heatmaps of the distribution of object parts. We use a heatmap to visualize the spatial distribution of the top-50 percent object parts in the $L$th layer of the explanatory graph with the highest inference scores. We also compare heatmaps with the grad-CAM ^[27] of the feature map. Unlike the grad-CAM, our heatmaps mainly focus on the foreground of an object and uniformly pay attention to all parts, rather than only focus on most discriminative parts.

We first trained/fine-tuned a CNN using object images of a category, which were cropped using object bounding boxes. Then, we set parameters $\tau \!=\!0.1$, $M\!=\!15$(except for results in Table 9), $T\!=\!20$, and $\beta \!=\!1$ to learn an explanatory graph for the CNN.

We learned explanatory graphs for the VGG-16, residual networks, and the VAE-GAN. We mainly extracted object parts from high conv-layers of these neural networks, because as discussed in ^[3], high conv-layers contain large-scale parts.

${\boldsymbol{\bullet }}$VGG-16: The VGG-16 was first pre-trained using the 1.3M images in the ImageNet dataset ^[25]. We then fine-tuned all conv-layers of the VGG-16 using object images in a category. The loss for fine-tuning was for binary classification between the target category and background images. The VGG-16 has thirteen conv-layers and three fully connected layers. We selected the ninth, tenth, twelfth, and thirteenth conv-layers of the VGG-16 as four valid conv-layers, and accordingly, we built a four-layer graph. We extracted $N_{d}$ nodes from the $d$th filter of the $L$th layer, where we set $N_{d}=40$ for all channels of the first and second conv-layers ($L=1$, or 2) and set $N_{d}=20$ for all channels of the third and fourth conv-layer ($L=3$, or 4).

${\boldsymbol{\bullet }}$Residual Networks: Two residual networks, i.e., the 50-layer and 152-layer ones, were used in experiments. The fine-tuning process for each network was exactly the same as that for VGG-16. We built a three-layer graph based on each residual network by selecting the last conv-layer with a $28\times 28\times 128$ feature output, the last conv-layer with a $14\times 14\times 256$ feature map, and the last conv-layer with a $7\times 7\times 512$ feature map as valid conv-layers. We set $N_{d}$ as 40, 20, and 10 for all channels in the first, second, and third conv-layers, respectively.

${\boldsymbol{\bullet }}$VAE-GAN: For each category, we used the cropped object images to train a VAE-GAN. We learned a three-layer graph based on all three conv-layers of the encoder of the VAE-GAN. We set $N_{d}$ as 52, 26, and 13 for all channels for the first, second, and third conv-layers, respectively.

4.2 Experiment 1: Part Visualization

The global structure of an explanatory graph for a VGG-16 network is visualized in Fig. 4. Fig. 12 shows the histogram of $P({\mathbf p}_{x}|{\mathbf p}_{V^{\prime }},{\boldsymbol{\theta }})$ values among all edges in an explanatory graph. In general, the distribution of $P({\mathbf p}_{x}|{\mathbf p}_{V^{\prime }},{\boldsymbol{\theta }})$ satisfied the assumption of the Gaussian distribution. Fig. 13 demonstrates the convergence of our method.

We visualized object parts of graph nodes from the following three perspectives.

Top-Ranked Patches . For each image $I$, we performed the part localization on its feature maps. For a node $V$, we extracted a patch at the location of ${\mathbf p}_{\hat{x}_{V}}$⁵ with a fixed scale of $70\;pixels\!\times \!70\;pixels$ to represent $V$. Fig. 5 shows a part’s image patches that had highest inference scores. In this figure, we used two different methods to infer the object part for each node. The first method was $\hat{x}={\arg \!\max }_{x\in {\mathbf X}:d_{x}=d}S_{V\rightarrow x}^{I}$ as mentioned before. The second method incorporated gradients to localize parts, i.e., $\hat{x}={\arg \!\max }_{x\in {\mathbf X}:d_{x}=d}|f_{x}\cdot \frac{\partial y}{\partial f_{x}}|$, where $y$ and $f_{x}$ denote the classification output of the target class and the activation value of the neural activation unit $x$, respectively. $|f_{x}\cdot \frac{\partial y}{\partial f_{x}}|$ is a classical evaluation of the numerical attribution of the neural activation unit $x$^[47].

Note that in this study, we assumed that the CNN was learned to classify a single category from random images. However, it would be quite interesting if we visualized graph nodes corresponding to a CNN encoding parts of multiple categories. To this end, we learned a VGG-16 network to classify six animal categories (bird, cat, cow, dog, horse, sheep ) from other fourteen categories in the VOC Part dataset ^[5] and built an explanatory graph for the CNN. Fig. 5 also visualizes nodes in this explanatory graph. Each node usually represented parts that were shared by multiple categories

Heatmaps of the Distribution of Object Parts . Given part localization results w.r.t. a cropped object image $I$, we drew heatmaps to show the spatial distribution of the inferred parts. We drew a heatmap for each layer $L$ of the graph. Each part $V\in \Omega$ was visualized as a weighted Gaussian distribution $\alpha \cdot {\mathbf{\mathcal N}}(\mu ={\mathbf p}_{V},\sigma _{V}^2)$⁵ on the heatmap, where $\alpha =S_{V\rightarrow \hat{x}}^{I}$. Fig. 6 shows heatmaps of the top-50 percent parts with the highest scores of $S_{V\rightarrow \hat{x}}^{I}$. Due to the lack of the ground truth for explanations, it is difficult to evaluate the attribution/attention/saliency map of a neural network. In general, two terms have to be considered in the evaluation, i.e., (1) whether or not the attribution map fits the human cognition and (2) whether or not the attribution map objectively reflects true reasons for the network prediction. From this perspective, in Fig. 6, results of the Grad-CAM better fit human cognition than our method. On the other hand, Fig. 6 visualizes the distribution of graph nodes, whose semantic meanings were verified in experiments. Therefore, the explanatory graph can better show object parts encoded in the CNN than the Grad-CAM method.

Fig. 7. Image synthesis based on the activation of nodes on an image. The explanatory graph only encodes major parts encoded in conv-layers with considerable information loss. Synthesis results demonstrate that the nodes are automatically learned to represent foreground appearance, and ignore background noises and trivial details of objects.

Node-Based Image Synthesis . We used the up-convolutional network ^[6] to visualize parts of graph nodes. Given an object image $I$, we used the explanatory graph for part localization, i.e., assigning each node $V$ with a certain neural activation unit $\hat{x}_{V}$ as its position inference⁵. We considered the top-10 percent nodes with highest scores of $S_{V\rightarrow \hat{x}}^{I}$ as valid ones. We filtered out all neural responses of units, which were not assigned to valid nodes, from feature maps (setting these responses to zero). We selected the filtered feature map corresponding to the second graph layer and used the up-convolutional network to synthesize the filtered feature map to the input image. Fig. 7 shows image-synthesis results, which can be regarded as the visualization of the inferred nodes.

Fig. 8. Purity of part semantics (top-left). We compared object parts corresponding to nodes in the explanatory graph with features of raw filters. We draw raw feature maps of filters (left), the highest activation peaks on feature maps of filters (middle), and image regions corresponding to each node in the explanatory graph (right). Based on such visualization results, we use human users to annotate the semantic purity of each node/filter.

4.3 Experiment 2: Semantic Interpretability of Nodes

In this experiment, we evaluated whether or not each node consistently represented the same object part through different images. Four explanatory graphs were built for a VGG-16 network, two residual networks, and a VAE-GAN. These networks were learned using the CUB200-2011 dataset ^[38]. We used the following two metrics to measure the interpretability of nodes.

Part Interpretability of Nodes . The evaluation metric was inspired by Zhou et al. ^[52]. For each given node $V$, we used $V$ to localize object parts among all images. We regarded inference results with the top-$K$ inference scores $S_{V}^{I_{i}}$ among all images as valid representations of $V$. We required the $K$ highest inference scores $S_{V}^{I_{i}}$ on images $\lbrace I_1,\ldots,I_{k}\rbrace$ to take about 30 percent of the inference energy, i.e., we use $\sum _{i=1}^{K}S_{V}^{I_{i}}=0.3\sum _{i\in {\mathbf I}}S_{V}^{I}$ to compute $K$. We asked human raters to count the number of inference results, which described the same object part, among the top $K$, in order to compute the purity of part semantics of node $V$. In addition, as mentioned before, $|f_{x}\cdot \frac{\partial y}{\partial f_{x}}|$ is a classical evaluation of the numerical attribution of the neural activation unit $x$^[47]. Thus, we designed a baseline method, namely Ours with top-ranked $|f_{x}\cdot \frac{\partial y}{\partial f_{x}}|$ , to select inference results with top-ranked $|f_{x}\cdot \frac{\partial y}{\partial f_{x}}|$ values that took 30 percent of the total $|f_{x}\cdot \frac{\partial y}{\partial f_{x}}|$ score of all images.

The table in Fig. 8(top-left) shows the semantic purity of the nodes in the second layer of the graph. Let the second graph layer correspond to the $L$th conv-layer with $D$ filters. The raw filter maps baseline used all neural activation in the feature map of a filter to describe a part. The raw filter peaks baseline considered the highest peak on a filer’s feature map as the part detection. Like our method, the two baselines also visualized top-$K^{\prime }$ part inferences (the $K^{\prime }$ feature maps’ neural activations took 30 percent of activation energies over all images). We back-propagated the center of the receptive field of each neural activation to the image plane and draw the image region corresponding to each neural activation. Fig. 8 compares the image region corresponding to each graph node and image regions corresponding to feature maps of each filter. Our graph nodes represented explicit object parts, but raw filters encoded mixed semantics.

Fig. 9. Notation for the computation of location instability.

Because the baselines simply averaged the semantic purity among the $D$ filters, we also computed average semantic purities using the top-$D$ nodes with the highest scores of $\sum _{i\in {\mathbf I}}S_{V}^{I}$ to enable a fair comparison.

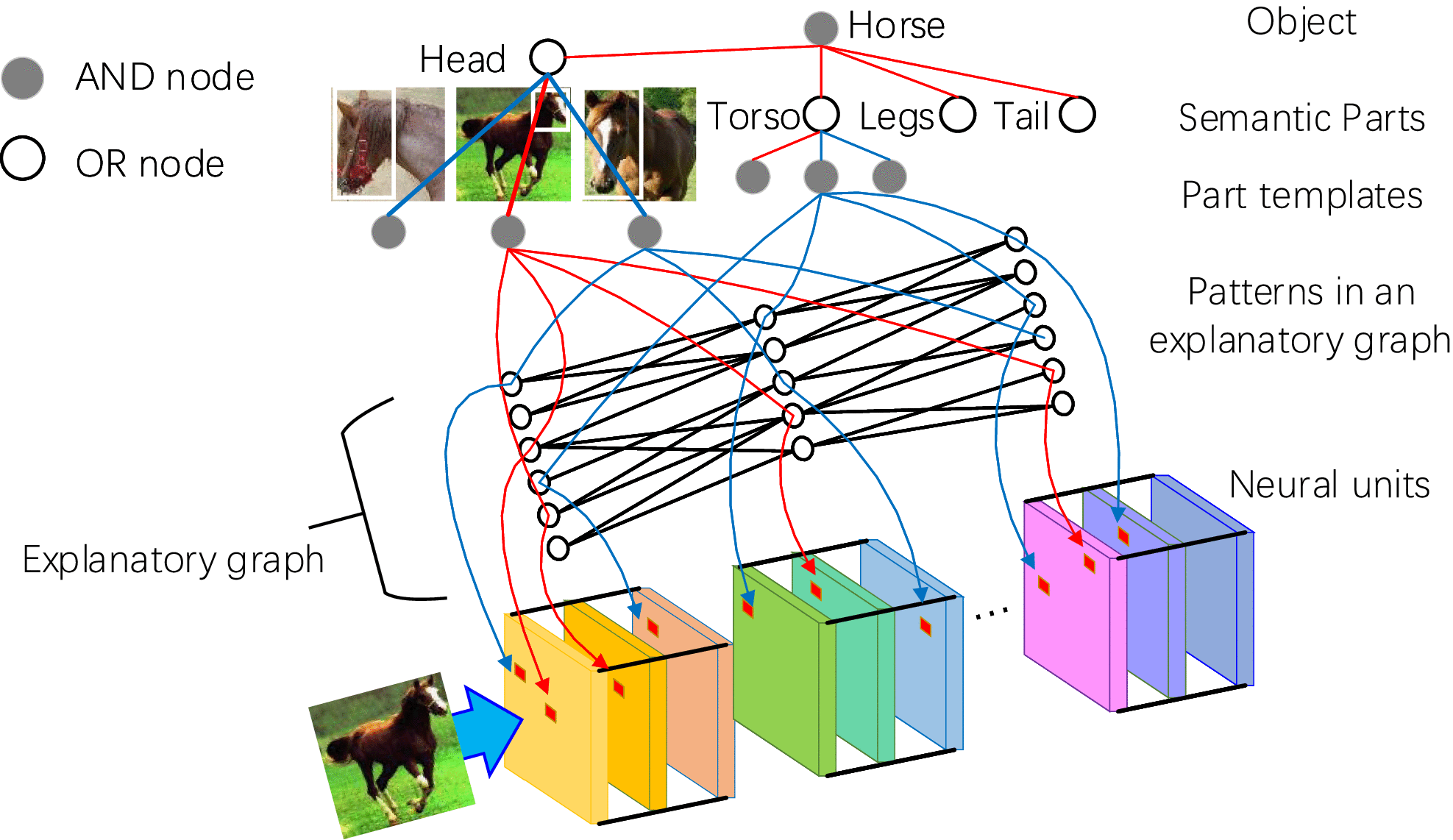
Fig. 10. Schematic illustration of an And-Or graph for semantic object parts. The AOG encodes a four-layer hierarchy for each semantic part, i.e., the semantic part (OR node), part templates (AND node), latent parts (OR nodes, those from the explanatory graph), and neural activation units (terminal nodes). In the AOG, the OR node of semantic part contains a number of alternative appearance candidates as children. Each OR node of a latent part encodes a list of neural activation units as alternative deformation candidates. Each AND node (e.g., a part template) uses a number of latent parts to describe its compositional regions.

Location Instability of Inference Positions . We defined the location instability for each node as another evaluation metric of interpretability. Note that we used the localization of object parts, rather than the localization of entire objects, to evaluate the clarity of semantic meanings of each node. We assumed that if a node was always activated by the same object part through different images, then the distance between the node’s inference position and a ground-truth landmark of the object part should not change a lot among various images.

As Fig. 9 shows, given a testing image $I$, $d_{I}^{\mathrm {head}}$, $d_{I}^{\mathrm {back}}$, and $d_{I}^{\mathrm {tail}}$ denote the distances between the inferred position of $V$ and ground-truth landmark positions of head , back , and tail parts, respectively. These distances were normalized by the diagonal length of input images. Then, the node’s location instability was given as $(\sqrt{var(d_{I}^{\mathrm {head}})}+\sqrt{var(d_{I}^{\mathrm {back}})}+\sqrt{var(d_{I}^{\mathrm {tail}})})/3$, where $var(d_{I}^{\mathrm {head}})$ denotes the variation of $d_{I}^{\mathrm {head}}$ over different images.

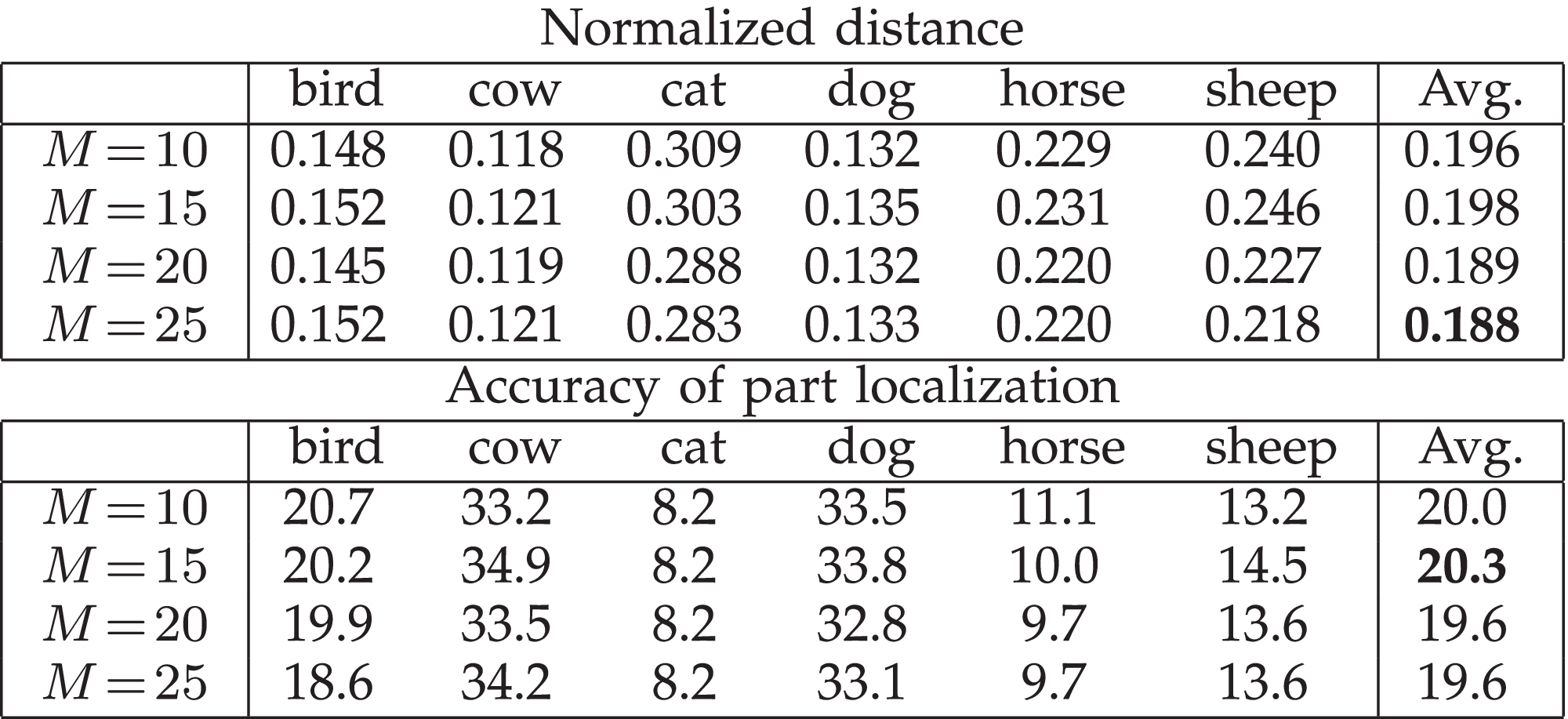
We compared its location instability of an explanatory graph with three baselines. The first baseline treated each filter in a CNN as a detector of a certain part. Thus, given the feature map of a filter (after the ReLu operation), we used the method of ^[52] to localize the unit with the highest response value as the part position. The other two baselines were typical methods to extract middle-level features from images ^[33] and extract parts from CNNs ^[30], respectively. For each baseline, we chose the top-500 parts, i.e., 500 nodes with top scores in the explanatory graph, 500 filters with strongest activations in the CNN, and the top-500 middle-level features. For each node, we selected position inferences on the top-20 images with highest scores to compute the location instability. Table 2 compares the location instability of different baselines. Nodes in the explanatory graph had significantly lower location instability than baselines.

4.4 Experiment 3: Few-Shot Part Localization

4.4.1 Hybrid And-Or Graph for Semantic Parts

The explanatory graph makes it plausible to transfer intermediate-layer features of a CNN to semantic object parts. In this section, we further designed a hybrid And-Or graph (AOG) to connect the explanatory graph, and the AOG associated nodes in the explanatory graph with explicit part names.

We used the AOG to test the transferability of nodes in the explanatory graph. It is because the AOG has been demonstrated as a classical model, which is suitable for representing the compositional hierarchy of objects ^[28],[54]. Adapting nodes in the explanatory graph enabled us to evaluate the clarify of compositional hierarchy that was encoded in a pre-trained CNN.

The structure of the AOG is inspired by ^[48], and the learning of the AOG was originally proposed in ^[44]. As Fig. 10 shows, the AOG encodes a four-layer hierarchy for each semantic part, i.e., the semantic part (OR node), part templates (AND node), latent parts (OR nodes, i.e., nodes in the explanatory graph), and neural activation units (terminal nodes).

where latent parts correspond to nodes from the explanatory graph.

In the AOG, each OR node (e.g., a semantic part or a latent part) contains a list of alternative appearance (or deformation) candidates. Each AND node (e.g., a part template) uses a number of latent parts to describe its compositional regions.

• The OR node of a semantic part contains a total of $m$ part templates to represent alternative appearance or pose candidates of the part.
• Each part template (AND node) retrieve $K$ latent parts from the explanatory graph as children. These latent parts describe compositional regions of the part.
• Each latent part (OR node) has all units in its corresponding filter’s feature map as children, which represent its deformation candidates on image $I$.

Technical Details . Based on the AOG, we use the extracted latent parts to infer semantic parts in a bottom-up manner. We first compute inference scores of different units at the bottom layer w.r.t. different latent parts, and then we propagate inference scores up to the layers of part templates and the semantic part for part localization.

The top OR node of the semantic part $V^{\mathrm {sem}}$ contains a total of $m$ part templates to represent alternative appearance or pose candidates of the part. We manually define the composition of the $M$ part templates. During part-inference process, given an image $I$, $V^{\mathrm {sem}}$ selects its best child as the true part template: $$\begin{equation*} \begin{split} S_{V^{\mathrm {sem}}}&=\mathop{\max} _{V^{\mathrm {tmp}}\in Child(V^{\mathrm {sem}})}S_{V^{\mathrm {tmp}}}\\ {\mathbf p}_{V^{\mathrm {sem}}}&={\mathbf p}_{\hat{V}^{\mathrm {tmp}}}, \end{split} \tag{5} \end{equation*}$$ where $S_{V^{X}}, X\in \lbrace \mathrm {sem,tmp,lat,unit}\rbrace$ denotes the inference score of $V^{X}$.

Then, each part template $V^{\mathrm {tmp}}$ uses a number of latent parts to describe sub-regions of the part. In the scenario of one-shot learning, we only annotate one part sample belonging to the part template. Then, we retrieve latent parts (nodes) that are related to the annotated part from all nodes in the disentangling graph. Given the inference score $S_{V^{\mathrm {lat}}}$ and inferred position ${\mathbf p}_{V^{\mathrm {lat}}}$ of each latent part $V^{\mathrm {lat}}$ on $I$, we retrieve the top $K$ latent parts with the highest scores of $S_{V^{\mathrm {lat}}}{\mathcal N}({\mathbf p}_{V^{\mathrm {lat}}}|\mu ={\mathbf p}_{V^{\mathrm {tmp}}}^{*},\sigma ^2)$ as children of $V^{\mathrm {tmp}}$. ${\mathbf p}_{V^{\mathrm {tmp}}}^{*}$ denotes the annotated position of the part $V^{\mathrm {tmp}}$; $\sigma ^2=(0.3\times \!image\;width)^2$ is a constant variation.

When we have extracted a set of latent parts for a part template, given a new image, we can use inference results of the latent parts to localize the part template: $$\begin{equation*} \begin{split} S_{V^{\mathrm {tmp}}}&=\sum _{V^{\mathrm {lat}}\in Child(V^{\mathrm {tmp}})}S_{V^{\mathrm {lat}}}\\ {\mathbf p}_{V^{\mathrm {tmp}}}&=\underset{V^{\mathrm {lat}}\in Child(V^{\mathrm {tmp}})}{\mathrm {mean}}\big \lbrace {\mathbf p}_{V^{\mathrm {lat}}}+\Delta {\mathbf p}_{V^{\mathrm {lat}},V^{\mathrm {tmp}}}\big \rbrace \end{split} \tag{6} \end{equation*}$$ where $\Delta {\mathbf p}_{V^{\mathrm {lat}},V^{\mathrm {tmp}}}$ denotes a constant displacement from $V^{\mathrm {lat}}$ to $V^{\mathrm {tmp}}$.

Each latent part $V^{\mathrm {lat}}$ has a channel of units as children, which represent its deformation candidates on image $I$. The score of each unit $x$ is given as $S_{V^{\mathrm {lat}}\rightarrow x}=F(x)P({\mathbf p}_{x}|V^{\mathrm {lat}},{\mathbf R},{\boldsymbol{\theta }})$. The OR node of $V^{\mathrm {lat}}$ selects the unit with the maximum score as its deformation configuration: $$\begin{equation*} \begin{split} S_{V^{\mathrm {lat}}}&={\max }_{x:V^{\mathrm {lat}}\in \Omega _{d_{x}}}\;S_{V^{\mathrm {lat}}\rightarrow x}\\ {\mathbf p}_{V^{\mathrm {lat}}}&={\mathbf p}_{\hat{x}}. \end{split} \tag{7} \end{equation*}$$ Please see ^[44] for details of the AOG.

4.4.2 Experimental Settings of Three-Shot Learning

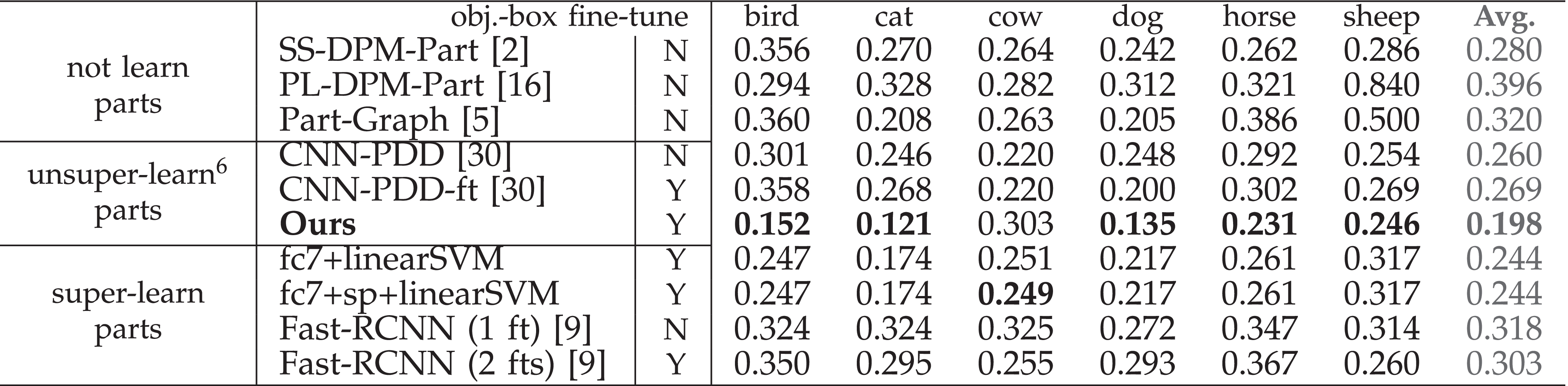
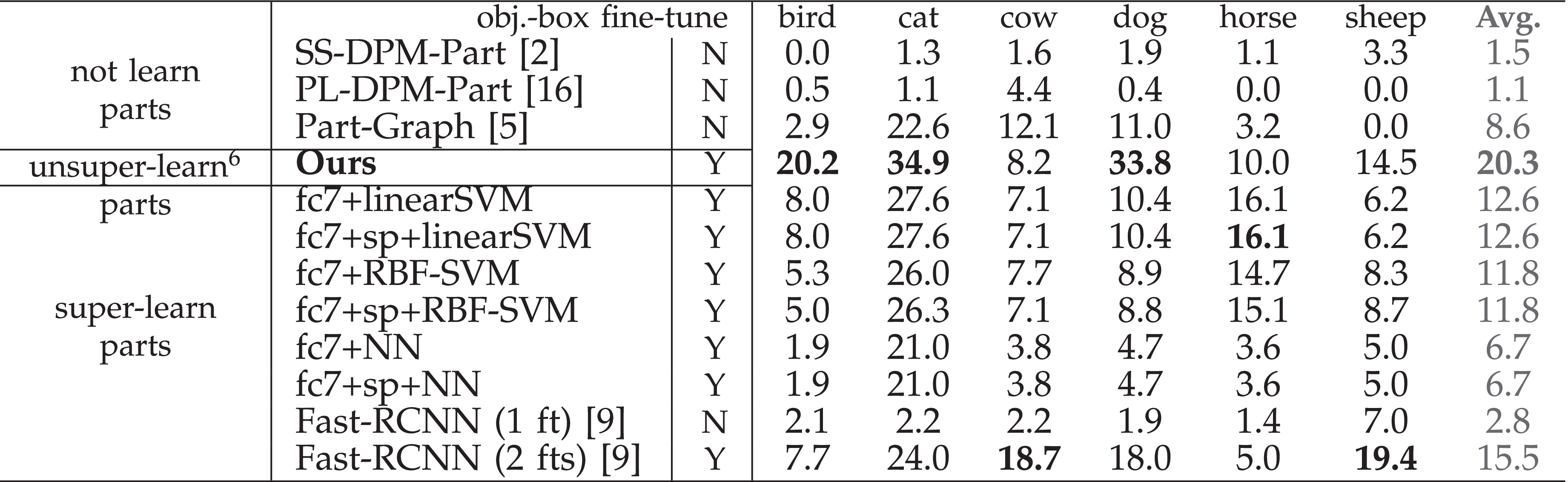
Given a fine-tuned VGG-16 network, we learned an explanatory graph and built the AOG upon the explanatory graph following the scenario of few-shot learning in ^[44]. For each category, we set three templates for the head part ($m=3$) and used three part-box annotations for the three templates. Note that we used object images without part annotations to learn the explanatory graph, and we used three part annotations provided by ^[44] for each part to build the AOG. All these object-box annotations and part annotations were equally provided to all baselines to enable fair comparisons (besides part annotations, all baselines also used object annotations contained in the datasets for learning). We set $K=0.1\sum _{L,d}N_{L,d}$ to learn AOGs for categories in the ILSVRC Animal-Part and CUB200 datasets and set $K=0.4\sum _{L,d}N_{L,d}$ for VOC Part categories. Then, we used the AOGs to localize semantic parts on objects.

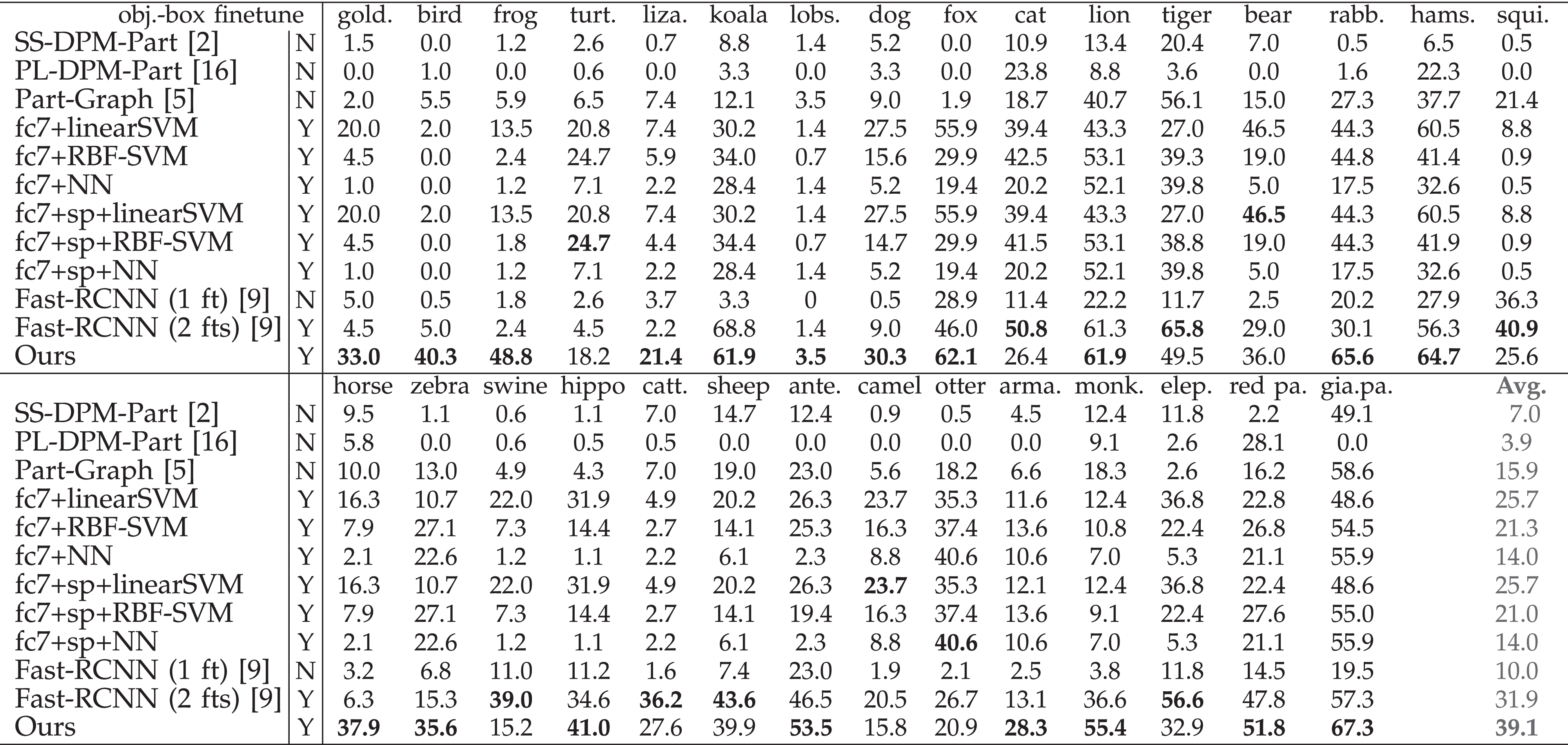
Baselines . We compared AOGs with a total of fourteen baselines for part localization. The baselines included (i) approaches for object detection (i.e., directly detecting target parts from objects), (ii) graphical/part models for part localization, and (iii) the methods selecting CNN features to describe object parts.

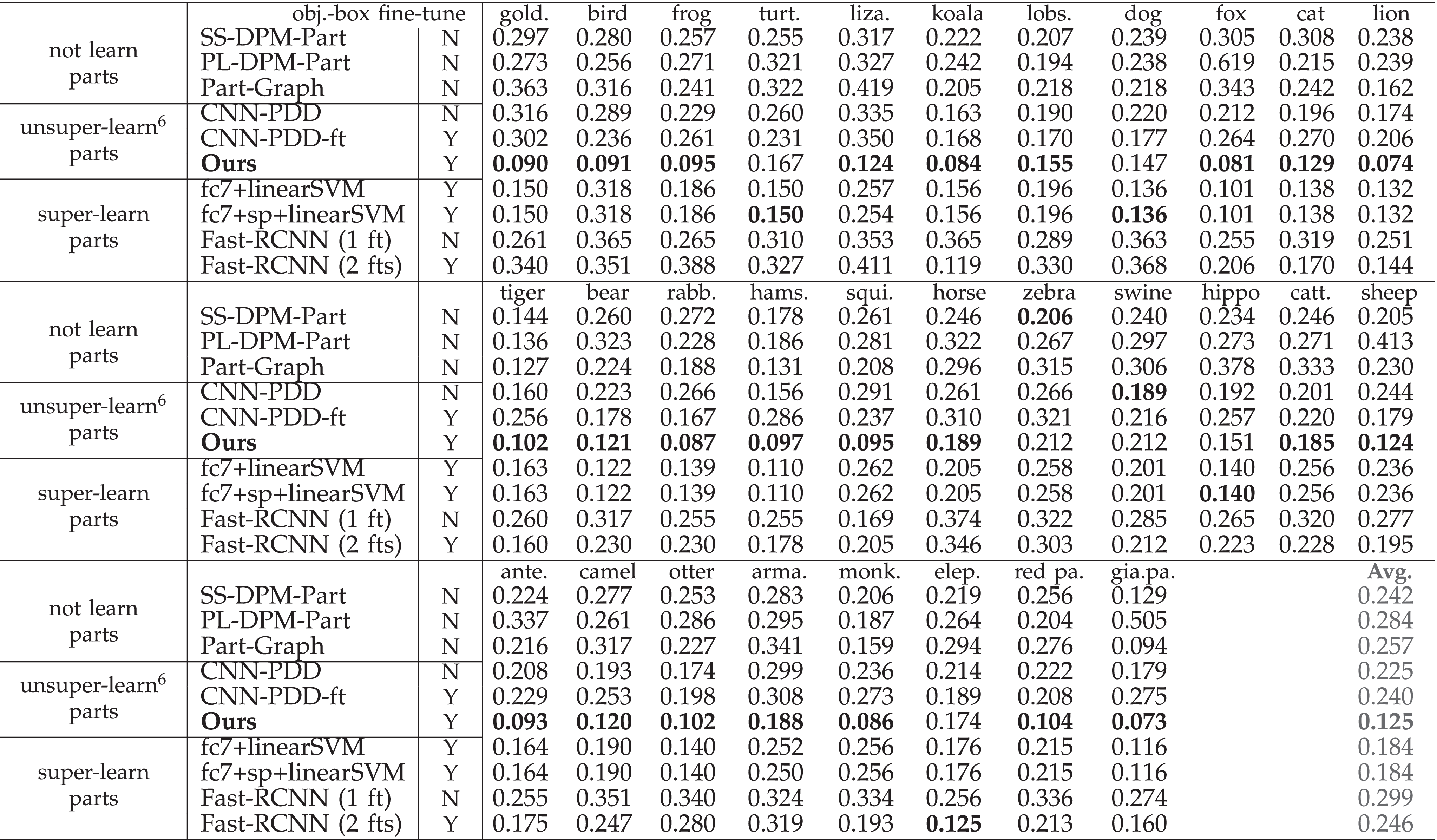
The first baseline was the standard fast-RCNN ^[9], namely Fast-RCNN (1 ft) , which directly fine-tuned a VGG-16 network based on part annotations. Then, the second baseline, namely Fast-RCNN (2 fts) , first used massive object-box annotations in the target category to fine-tune the VGG-16 network with the loss of object detection. Then, given part annotations, Fast-RCNN (2 fts) further fine-tuned the VGG-16 to detect object parts. We used ^[30] as the third baseline, namely CNN-PDD . CNN-PDD selected certain filters of a CNN to localize the target part. In CNN-PDD, the CNN was pre-trained using the ImageNet dataset ^[25]. Just like Fast-RCNN (2 ft), we extended ^[30] as the fourth baseline CNN-PDD-ft , which fine-tuned a VGG-16 network using object-box annotations before applying the technique of ^[30]. The fifth and sixth baselines were DPM-related methods, i.e., the strongly supervised DPM (SS-DPM-Part ) ^[2] and the technique in ^[16] (PL-DPM-Part ), respectively. Then, the seventh baseline, namely Part-Graph , used a graphical model for part localization ^[5]. For weakly supervised learning, “simple” methods are usually insensitive to model over-fitting. Thus, we designed six baselines as follows. First, we used object-box annotations in a category to fine-tune the VGG-16 network. Then, given a few well-cropped object images, we used the selective search ^[36] to collect image patches, and used the VGG-16 network to extract fc7 features from these patches. The baselines fc7+linearSVM , fc7+RBF-SVM , fc7+NN used a linear SVM, an RBF-SVM, and the nearest-neighbor method (selecting the patch closest to the annotated part), respectively, to detect the target part. The other three baseline fc7+sp+linearSVM , fc7+sp+RBF-SVM , fc7+sp+NN combined both the fc7 feature and the spatial position $(x,y)$ ($-1\leq x,y\leq 1$) of each image patch as features for part detection. The last competing method is weakly supervised mining of parts from the CNN ^[44], namely supervised-AOG . Unlike our method (unsupervised), supervised-AOG used part annotations to extract parts.

Comparisons . We divided all baselines into three groups. The first group, namely not-learn parts , included traditional methods without using deep features, such as SS-DPM-Part, PL-DPM-Part, and Part-Graph. These methods did not learn deep features⁶. The second group, termed super-learn parts , contained Fast-RCNN (1 ft), Fast-RCNN (2 ft), CNN-PDD, CNN-PDD-ft, supervised-AOG, fc7+linearSVM, and fc7+sp+linearSVM. These methods learned deep features using part annotations, e.g., fast-RCNN methods used part annotations to learn features; supervised-AOG used part annotations to select filters from the CNN to localize parts. The third group (unsuper-learn parts ) included CNN-PDD, CNN-PDD-ft, and our method. These methods learned deep features using object-level annotations, rather than part annotations.

Fig. 11. Localization results based on AOGs that are learned using three annotations of the head part.

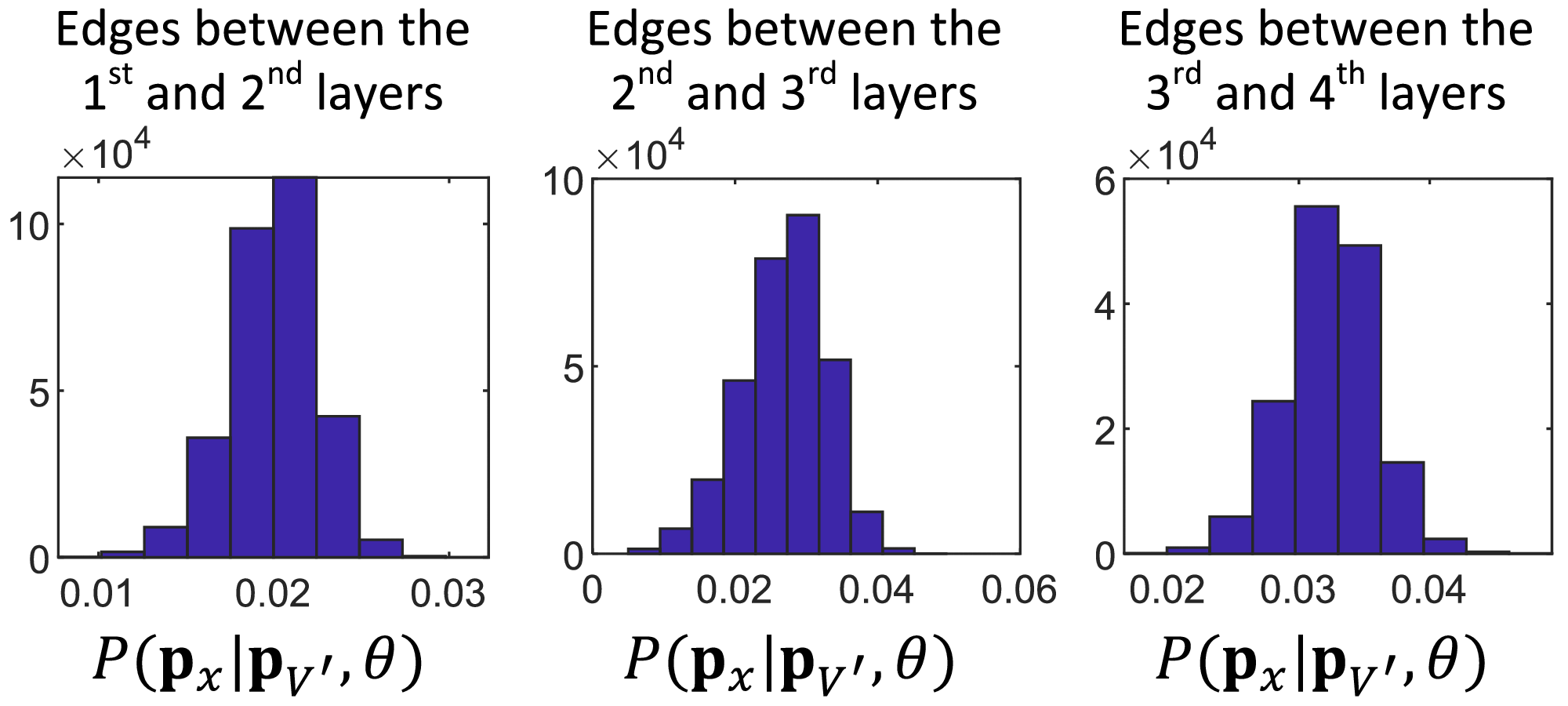
Fig. 12. Histogram of $P({\mathbf p}_{x}|{\mathbf p}_{V^{\prime }},{\boldsymbol{\theta }})$ values among all edges in an explanatory graph for the cat category.

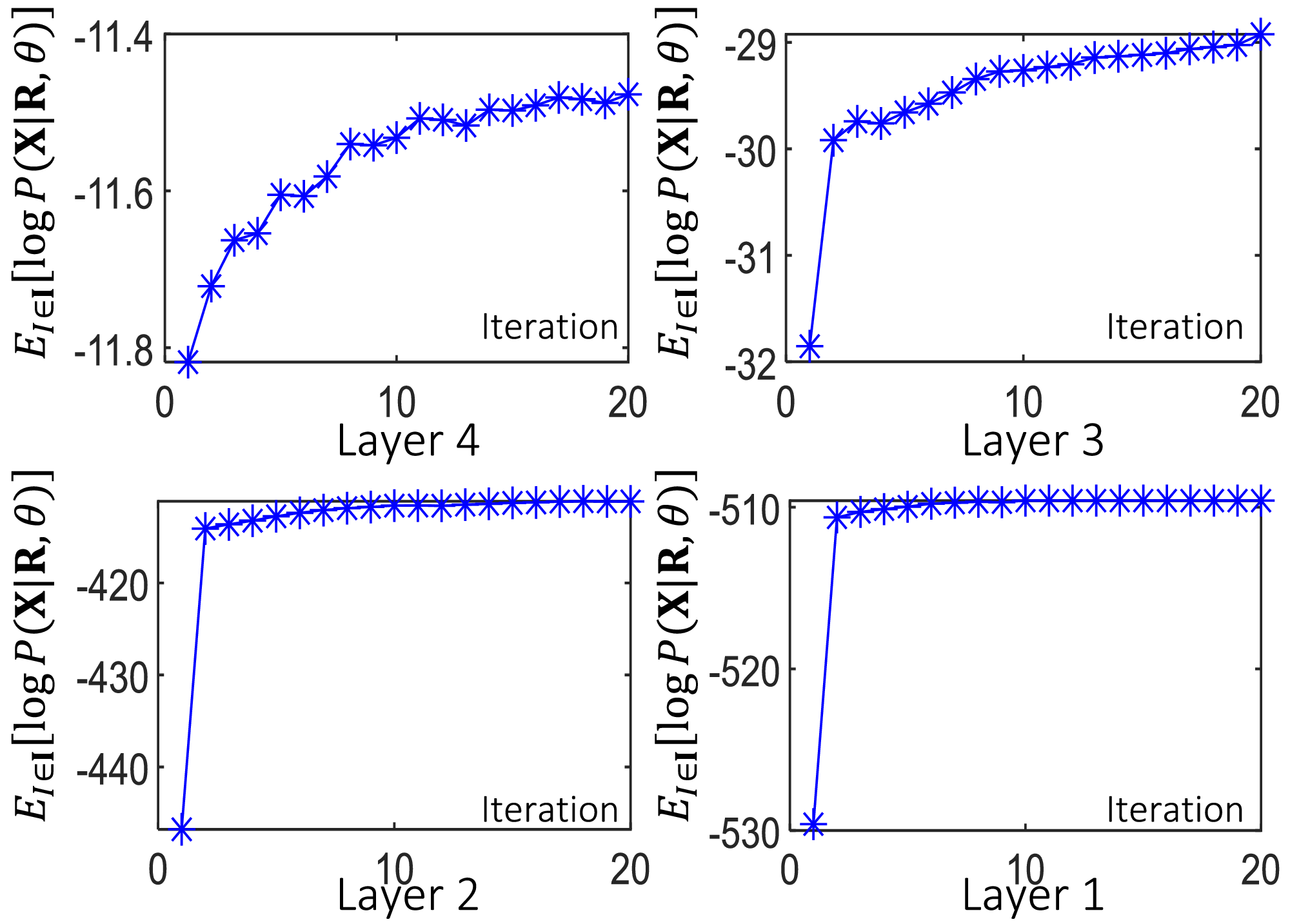
Fig. 13. Convergence of the learning process. We showed the average value of $\log P({\mathbf X}^{I}|{\mathbf R}^{I},{\boldsymbol{\theta }})$ after different iterations during the learning process.

Fig. 11 visualizes localization results based on AOGs, which were learned using three annotations of the head part of each category. We used the normalized distance (used in ^[30],[44]) and the traditional intersection-over-union (IoU) criterion to evaluate the localization performance. Tables 3,4,5,6, and 7 show part-localization results on the CUB200-2011 dataset ^[38], the VOC Part dataset ^[5], and the ILSVRC 2013 DET Animal-Part dataset ^[44]. AOGs based on our graph nodes exhibited outperformed all baselines in few-shot learning. Note that our AOGs simply localized the center of an object part without sophisticatedly modeling the scale of the part. Thus, detection-based methods, which also estimated the part scale, performed better in very few cases. Table 8 compares the unsupervised and supervised learning of parts. In the experiment, our method outperformed all baselines, even including approaches that learned part features using part annotations. Finally, Table 9 compares the part-localization performance when we set different edge numbers $M$ for each node. It shows that explanatory graphs with each node containing 15 edges usually performed better in the perspective of the intersection-over-union (IoU) criterion, and explanatory graphs with each node containing 25 edges exhibited lower normalized distances of part localization.

Note that we tested the explanatory graph and its corresponding AOG from the perspective of part localization, instead of evaluating their performance of object recognition. It is because the explanatory graph was proposed to explain object-part semantics in intermediate layers of the CNN, and the AOG was designed for part localization (i.e., estimating the part location under the condition that the image contains the target part), instead of object recognition (i.e., identifying whether or not the target object appears). Moreover, theoretically, it was difficult for nodes in the explanatory graph to outperform the original CNN, because the explanatory graph selectively retrieved part-alike neural activations from high conv-layers, and ignored other activations, whereas fully-connected layers in the CNN used all information (including both object parts and textures) to recognize objects. I.e., the original CNN used much richer information than the explanatory graph.

5   Conclusion and Discussions

In this paper, we have developed a simple yet effective method to learn an explanatory graph that reveals the compositional hierarchy of object parts encoded inside conv-layers of a pre-trained CNN. The explanatory graph filters out noisy activations, disentangles object parts from each filter, and models co-activation relationships and spatial relationships between parts. Experiments showed that our graph nodes had significantly higher stability than baselines. More crucially, our method can be applied to different types of networks, including the VGG-16, residual networks, and the VAE-GAN, to explain their conv-layers.

The transparent representation of the explanatory graph boosts the transferability of CNN features. Part-localization experiments well demonstrated the good transferability of graph nodes. Our method even outperformed the supervised learning of part representations. Nevertheless, the explanatory graph is just a rough representation of the CNN. It is still difficult to well disentangle textural patterns from filters of the CNN.