Efficient Cryo-Electron Tomogram Simulation of Macromolecular Crowding with Application to SARS-CoV-2

I.   Introduction

Cryo-Electron Tomography (cryo-ET) is an important and powerful tool which can reveal the in situ status of subcelluar structures and intercelluar environments with high resolution (1-2 nm) ^[3]. To extract more useful information in cryo-ET, machine learning methods are applied in several analyzing tasks including classification, segmentation and localization, etc. Even though machine learning methods have been shown to be able to extract more informative features than human eyes, the analyzing process is still very difficult due to the super-crowded subcellular status and low Signal-to-Noise-Ratio(SNR). Besides, since most of the existing methods are supervised, their performance is limited because it is hard to obtain labeled training data ^[13]. Therefore, the realistic simulation of cryo-ET images is urgently needed. The simulated cryo-ET images are pre-labeled, which provides a basis for the introduction of supervised machine learning methods.

Some methods simulate the isolated macromolecules ^[28], and are already been used to assist subtomogram classification and averaging. However, due to the lack of neighboring macromolecules, it is not sufficient to show the crowded status in the cell ^[10], and thus the assistance is limited. It is also not suitable for localization tasks focusing on multiple structures. Other simulation methods focus on dynamic simulations for multiple macromolecules ^[17], but they are very time consuming and are not suitable for generating large amounts of data ^[6].

Fig. 1.Fig. 1. The process of macromolecule packing and cryo-ET simulation. (a) Four macromolecules are packed into a crowded status by moving them toward each other. They are randomly placed in a initial box with an automatically calculated size. (b) The target macromolecule (1BXN) and four random neighbors. (c) The 3D density map is then generated, and the slices are shown. (d) we added noise into the density map and obtain cryo-ET with different SNR.

Therefore, we propose a new efficient simulation framework for cryo-ET of macromolecular crowding, containing a target macromolecule and several random neighbor macromolecules, to fill the gaps in this field. We used gradient descent method to pack several macromolecules together, and then generated the noise-free 3D density maps according to the calculated coordinates and orientations. The final tomogram is obtained by simulate the actual tomographic image reconstruction process.

A global health crisis ascribed to the novel coronavirus disease (COVID-19) hits the world. The public health responses strived to slow the transmission of the pandemic and assistance to doctors in diagnosing and prognosing the disease is required. In an effort to contain the pandemic as soon as possible, many research laboratories are investigating into SARS-CoV-2, the virus responsible for COVID-19. Similar to other beta-coronaviruses, SARS-CoV-2 is composed of a viral membrane, various proteins embedded in the membrane or located inside the virus, and viral RNA genomes. The virus infects cells through the binding of the spike protein (S-Protein) on virus surface and its receptor called angiotensin-converting enzyme 2 (ACE2) on target cell membrane ^[16]. The structure of these proteins are crucial for understanding the mechanism of SARS-CoV-2 infection and replication. Since cryo-ET is a three-dimensional imaging technique being used to obtain nanometer-scale information of macromolecular complexes in their native environment, it is an ideal method to study viruses in light of their characteristics. Particularly, cryo-ET marked with crucial proteins can show detailed information about their distribution and interaction with host cells.

At present, diverse cryo-ET protein detection methods are mature, including template matching, 3D ResNet, U-net, etc. They can be adapted to aim at detecting SARS-CoV-2 related complexes, but virus based cryo-ET training data is lacking. So we apply the proposed simulation framework of macromolecule crowding to generate tomograms of SARSCoV-2 at near-native condition in an effort to assist detection and classification of virus related macromolecules. In the resulting tomograms, one SARS-CoV-2 virus is placed next to part of the host cell membrane and surrounded by its constituent proteins to simulate the scene of virus infection. The automatically generated virus samples could serve as a benchmark dataset to test developing algorithms and help to train supervised models for detecting and classifying vital virus macromolecules, which could then benefit researchers in tracking virus’ behaviors.

II.   Related Work

Cryo-electron tomography enables the imaging of the three-dimensional structure of macromolecular complexes at nano-resolution and at native conditions ^[18], thus it emerges as an effective tool for in situ structural biology. However, due to the low SNR of cryo-electron tomograms and the large amount of data, manual segmentation of the particles is rarely feasible and subjective results are unavoidable ^[14]. Instead, automated approaches are good alternatives. Template matching ^[12] is a typical approach for segmenting particles of known structures in the tomogram, during which a template is cross-correlated over a tomogram to find locations and angles where the template matches the most. By contrast, reference-free methods are used for particles with unknown structures. Applying Difference of Gaussian (DoG) ^[23] is the most common approach: a band-pass filter that removes noisy high frequency components and homogeneous low frequency areas, obtaining spatial information that lies in the range of preserved frequencies. The high-resolution structure of one particle can be obtained by aligning and averaging multiple copies of the same particle extracted from the tomogram. In recent years, approaches based on machine learning have been successfully applied to cryo-ET analysis. Classical support vector machines have been used for both detection and classification ^[9]. With increasing amounts of cryo-EM and ET data ^[1], deep learning methods provide faster and often more accurate results than template matching. Supervised methods were proposed for localization ^[24], classification ^[7], and end-to-end semantic segmentation ^[8]. One feature of supervised deep learning methods is their heavy dependence on annotated data, but it is time consuming to manually annotate all particles in a tomogram by experts. This problem leads to researches developing techniques for the automatic simulation of cryo-ET images with pre-specified labels.

Fig. 2.Fig. 2. The simulation of the virus and several ACE2 protein next to a cell membrane. (a) is the isosurface result of the simulated result. (b) is a slice of noise-free density map. (c) are two simulated tomogram under different SNRs. (d) shows all the proteins used in this scene.

The typical approach of simulating tomographic images is first to calculate the density map from atomic structures and then add distortions to the density map due to the missing wedge effect, interactions between electrons and the specimen, as well as introduced by image detectors ^[25]. The crowded nature in cells makes macromolecular segmentation and detection a challenging task ^{[5],[12],[25]}. Most current simulation methods generate simulated subtomograms with a single macromolecule or macromolecules distributed randomly in a rectangular box, which can be widely used to assess template matching and subtomogram classification and averaging ^{[2],[11],[25]}. In order to perform particle picking in realistic imaging conditions and gain the most optimized parameters, we need to first simulate cryo-electron tomograms of crowded macromolecular complex clusters close to native status. The previous work ^[25] generated crowded mixtures by utilizing molecular dynamics simulations and simulated annealing to optimize the packing of the crowded mixture of spheres and then remove any sphere-sphere overlaps. This method applied a complex loss function, which requires a large amount of computation. M. Chavent et al. ^[6] proposed an approach to realize molecular dynamics simulations of crowded membrane proteins and their interactions, but molecular dynamics based simulation takes too much time and details of protein–lipid interaction are not necessary for macromolecule detection analysis. A simpler and faster realistic simulation method of crowded macromolecule images is needed.

Severe acute respiratory syndrome coronavirus 2 (SARSCoV-2) is the causative agent of the COVID-19 pandemic. In an effort to contain the pandemic as soon as possible, many research laboratories are investigating into SARS-CoV-2. S. Klein et al. ^[16] reported critical insights into the budding mechanism of the virus and provide structural details of virions by in situ cryo-electron tomography. Coronaviruses are composed of the glycoprotein spikes (S-Protein), the transmembrane protein (M-Protein), the encelope small membrane protein (E-Protein) and the nucleoprotein (N-Protein), which forms a viral ribonucleoprotein complex with the viral RNA. During the infection process, SARS-CoV-2 binds to the angiotensin-converting enzyme 2 (ACE2) receptor present on the cell surface of permissive cells. Several works also describe the binding behavior of related vital proteins ^[21],[22]. In accordance with ^[22], the S-Protein of SARS-CoV2 is a key component for cell entry and is the major focus for vaccine development. The paper structurally analyze S in cryo-ET. J. Shang et al. ^[21] illustrate that SARS-CoV-2 and SARS-CoV recognize the same receptor ACE2 in humans and determined the crystalline structure of the receptor-binding domain of S-Protein with ACE2. Evidence showed that S-Protein on SARS-CoV-2 and ACE2 on cell membrane were key proteins for infection. We use these researches to build the structure of SARS-CoV-2 in order to design a realistic scene of virus infection.

Data of native SARS-CoV-2 in cryo-ET are available thanks to previous researches. A cryo-ET dataset of purified virions has been published by ^[22], which contains large-scale raw data. However, since these tomograms are not acquired by simulation, it lacks particle picking or semantic segmentation ground-truth for many analysis works. Besides, with the small amount of labeled data, it is still difficult to support the training process of the supervised learning method because the relatively small amount of data will reduce the generalization ability of the model. Under increasing attention, some SARSCoV-2 simulation methods have been proposed. In ^[27], the authors simulated the coarse-grained model for SARS-CoV-2 virion with some of its constituent proteins and provides the model as a Protein Data Bank (PDB) file, which serves as the building blocks of our virus infection scene simulation. But one shortcoming of this model is that the virus has an empty core, which is not realistic because there should be N-Proteins and RNA. Moreover, the virion model is isolated and cannot represent the actual crowded environment around the virus in the human body. The simulation can be largely improved when the virus is put into richer scenes close to its native status, such as next to the host cells and surrounded by numerous other proteins. So we develop a virus infection simulation method as an application of our general macromolecular crowding packing framework.

Fig. 3.Fig. 3. The simulated cryo-ET of 50 macromolecules after packing. (a) is the 3D visualization which shows the spacial distribution of all packed proteins. (b) is the continuous slices of the 3D density map. (c) shows the slices of the simulated tomogram which is obtained based on the noise-free density map, (d) is an enlarged image of the selected density map slice, it is the one marked by the yellow box in (b). (e) is the enlarged tomogram slice corresponding to the marked on in (c).

III.   Efficient Packing For Cryo-Et Simulation

To simulate cryo-ET efficiently, we need to first simplify all the macromolecules into single spheres. These spheres will be randomly placed in a box and packed together using the gradient descent method. The final coordinates will be used to synthesize the 3D density map with the help of single density maps of all the macromolecules. The orientation is randomly set. The tomogram will be obtained by simulating the actual tomographic image reconstruction process including adding noise, tomographic distortions and electron optical factors.

A. Simplify Macromolecule to Sphere

We simplify all the macromolecules according to the information from their PDB files. All the macromolecules are represented by minimum boundary spheres with different radii. For a macromolecule P , the center of the boundary sphere is obtained by the mean value of the maximum and minimum atoms coordinate on X, Y, Z axis. Then the radius R_P of a specific macromolecule is calculated as the maximum Euclidean distance between an atom and the center.

B. Initialization

A target macromolecule and several random neighbor macromolecules are selected to generate the subtomogram. The number of neighbors is defined by the user. The size l of the cubic simulation scene is determined by the macromolecules number N and the largest boundary sphere R_max , that is: $$\begin{equation*}l=\lceil\sqrt{N}\rceil \cdot 2 R_{\max} \cdot k_{\text {first}} \cdot 10 \tag{1}\end{equation*}$$ where $k_{\text {first}}=1$ if the first digit of $\lceil\sqrt{N}\rceil \cdot 2 R_{\max}$ is smaller than 5 , and $k_{\text {first}}=5$ otherwise.

We then initialize all macromolecules with different locations by setting macromolecules’ centers randomly according to the box size. The overlap is avoided by forcing the Euclidean distance between two sphere centers to be greater than the sum of their radii.

C. Packing Macromolecules to Macromolecular Crowding

An efficient packing process is conducted based on the gradient descent algorithm, which moves the proteins toward each other without overlap. For each protein P_k , the loss function ${Loss}_{Pk}$ is defined as the sum of the Euclidean distances between a protein and its neighbors: $$\begin{equation*}\operatorname{Loss}_{P_{k}}=\sum_{i}^{N}\left(x_{i}-x_{k}\right)^{2}+\left(y_{i}-y_{k}\right)^{2}+\left(z_{i}-z_{k}\right)^{2} \tag{2}\end{equation*}$$ where $x_{i}, y_{i}$ and z_i is the coordinate of protein i . The gradient $(\operatorname{Grad} X, \operatorname{Grad} Y, \operatorname{Grad} Z)$ of the loss function is calculated by the partial derivative with respect to $x, y$ and z . Take $\operatorname{Grad} X$ as an example: $$\begin{equation*}\operatorname{Grad} X=\frac{\partial \operatorname{Los} s_{P_{k}}}{\partial x}=2\left[\sum_{i}^{N}\left(x_{i}-x_{k}\right)\right]=2\left[\sum_{i}^{N} x_{i}-N \cdot x_{k}\right] \tag{3}\end{equation*}$$

In each step, all the macromolecules will move in the direction of the vector (- GradX,- GradY,- GradZ ). The overlap detection will be performed during each step, and any overlap move will be rejected. The iterations will continue until the loss function converges. The packing process will be conducted multiple times to return the most optimal (crowded) result.

D. Simulate Density Map and Tomogram Generation

The final Density map is generated by combining the single density maps of all single macromolecules based on their PDB file, the final coordinate and a random orientation. The orientation is represented by Euler angle in $Z Y Z$ convention, which can be represented by a rotation matrix: $R=R_{z}(\alpha) R_{y}(\beta) R_{z}(\gamma)$ where R is the final rotation matrix, $\alpha, \beta$ and $\gamma$ are the rotation angle in three sub-process.

According to the actual tomographic image reconstruction process, a simulated cryo-ET is generated by adding noise, tomographic distortions and electron optical factors. Noise was added to achieve different SNR levels. The tomographic distortions are caused by missing wedge effect, which is due to the limited tile angle with range typically [- 60, [60]. We simulated 2D projection electron micrographs of the simulated sample using a tilt angle range from -60 to 60 degrees with step increments of 2 degrees. Then we reconstructed the cryo-ET via a back projection algorithm ^[4],[20]. For electron optical factors, Contrast Transfer Function (CTF) and Modulation Transfer Function (MTF) can be used to implement the distortions caused by the interaction between the sample and the electrons and the image detector. ^[25]. Here, MTF is $\operatorname{sinc}(\pi \omega / 2)$ where $\omega$ denotes the fraction of the Nyquist frequency ^[19]. In all the experiment, we set the voxel size equal to 1 nm, the spherical aberration equal to $2 \times 10^{-3} \mathrm{~m}$ and the defocus value equal to $-5 \times 10^{-6} \mathrm{m}$.

IV.   Sars-Cov-2 Tomogram Simulation

A SARS-CoV-2 virion and its constituent proteins are randomly selected as the primary content of subtomograms. We exploit the proposed packing algorithm to calculate these particles’ random locations. The particles are then placed according to their locations after a random rotation is used to generate the density map of SARS-CoV-2 surrounded by its constituent macromolecules. To give the virion a more realistic appearance, we fill the virus with nucleocapsid proteins (N-Protein), which are structural proteins that bind to the coronavirus RNA genome. N-Proteins are randomly distributed in a sphere with radius $R_{N}=\frac{1}{2} R_{\text {virus}}$.

To mimic the scene where the virus infects cells, we overlay the simulated cell membrane onto the resulting density map, which is part of a sphere with radius $R_{\text {cell}}. R_{\text {cell}}$ is determined by the size of the cubic simulation scene l , that is $R_{\text {cell}}=l$. The center of the cell membrane sphere is calculated to avoid the membrane crossing the virus. It can be represented by: $$\begin{equation*}O_{\text {cell}}=O_{\text {virus}}-\frac{\sqrt{3}}{3}\left(R_{\text {cell}}+R_{\text {virus}}\right)-d \tag{4}\end{equation*}$$ where $O_{\text {cell}}$, Ovirus are the center coordinates of the cell membrane and the virus, $d=(d 1, d 2, d 3) \in\left[0, \frac{1}{4} R_{\text {virus}}\right]^{3}$ is a three dimensional vector representing the random additional distance deviation between the cell and the virus centers. This way, the distance between the cell membrane and the virus is limited to a certain range where the binding is about to occur.

ACE2, the receptor for S-Protein, is evenly and randomly located on the cell membrane after a random rotation. The general density map of the virus and cell scene is obtained through a combination of the density maps of the packing result including the virus and its constituent macromolecules, the N-Proteins inside the virus, the cell membrane, and ACE2 on the cell surface.

V.   Experiment

We stimulated cryo-ET macromolecule crowding with our proposed approach. To test the packing effects with a different number of macromolecules, we packed the target macromolecule with 4 to 50 random neighbors. Besides, we generated the cryo-ET of SARS-CoV-2 next to the host cell membrane as a further application of our packing algorithm.

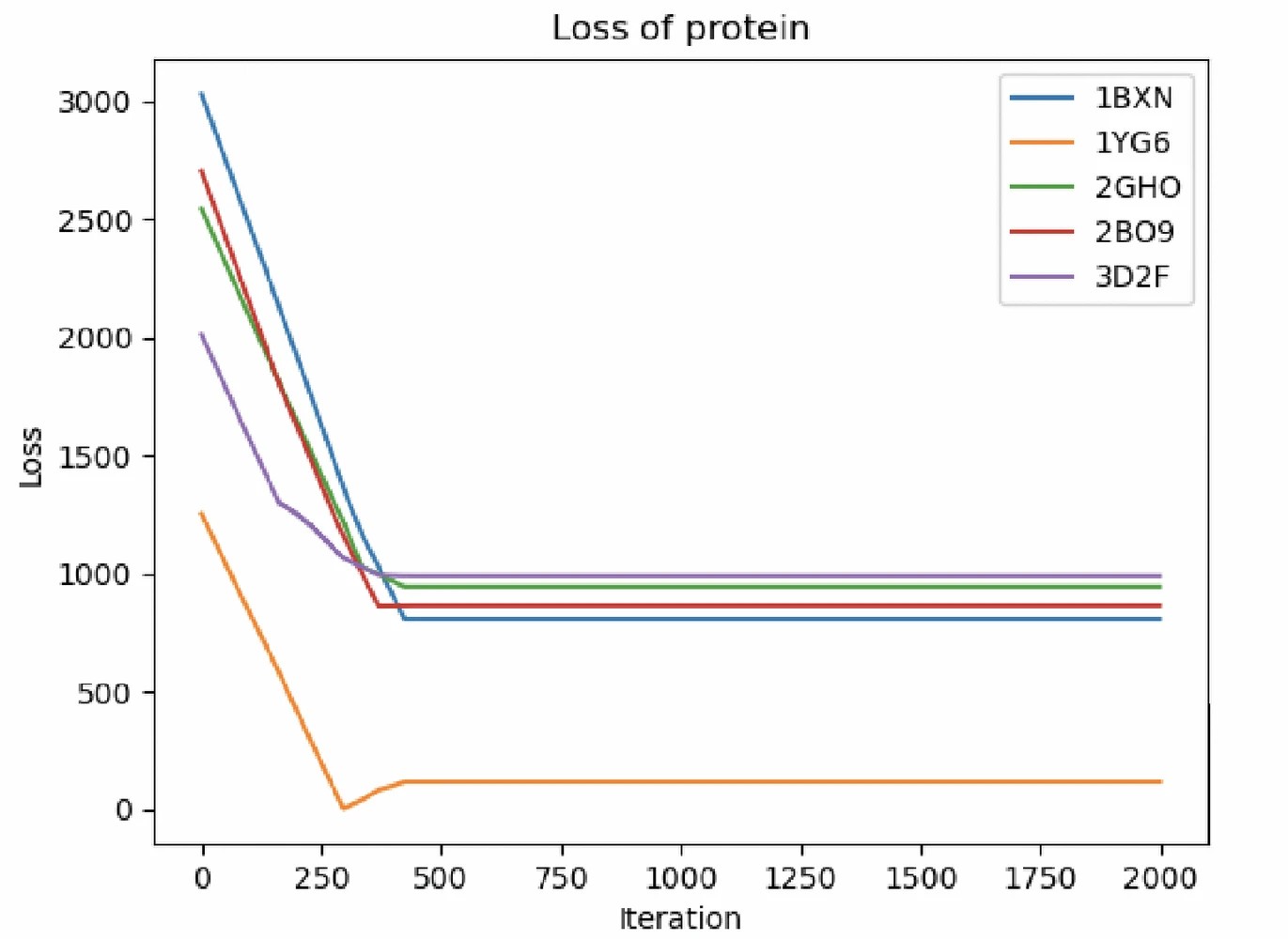
Fig. 4.Fig. 4. The loss function value in each step of the five selected proteins.

A. simulation of packed macromolecule crowded

We packed a target macromolecule (protein 1BXN) together with 4 random neighbors. The 3D visualization of a single protein and the packed macromolecules cluster volume are shown in Figure 1 (a) and (b). In this figure, we could see five structures right next to each other clearly. The value of the loss function during the packing process is shown in Figure 4. It could be seen that the loss function converged after 500 iterations. The sliced image of the simulated density map and the simulated cryo-ET with a different SNR is shown in Figure 1 (c) and (d). we also attached a video to show all the slices in the 3D volume dynamically.

The size of the simulation scene is $100 \ast 100 \ast 100$ voxels of size 1 nm. The packing process finished in 5 seconds, and the tomogram generation process finished in 5 seconds.

In a more realistic cellular scene, macromolecules are far more numerous. Therefore, we increased the number of neighboring proteins to 50 with 9 different types. The 3D visualization of the protein cluster is shown in 3 (a). We can see the locations of the proteins are concentrated but do not overlap. 3 (b) shows simulated density map slices, one slice of which is magnified in 3 (d). 3 (c) represents cryo-ET slices with a SNR rate of 1.0 and 3 (e) is one magnified slice of it. The size of the scene is 175³ . The resolution and the voxel size are both 1 nm.

B. SARS-CoV-2 Tomogram Simulation

In the SARS-CoV-2 simulation, we packed the virus with constituent proteins including M-Protein, S-Protein, and N-Protein, as well as the host cell receptor, ACE2. The total number of its neighbors is 10. We utilized the open source PDB file of the coarse-grained SARS-CoV-2 model published on github ^[27]. The 3D structure of a single virion, its constituent proteins, and ACE2 are visualized in 2(d). As shown in Figure 2(a), the host cell membrane appears in the upper left corner of the scene. An outer layer of ACE2 surrounds the thinner membrane, which is actually the receptor protein embedded on the host cell surface. The shadow inside the virus represents its internal proteins and RNA genomes and is composed of randomly located Nucleoproteins. The 3D visualization of simulation result is shown in Figure 2(a). As you can see, the isolated particles beside the virus are its packing neighbors. One slice of simulated 3D density map is shown in Figure 2(b). Example slices of simulated cryo-ET image with different SNR rates are shown in Figure 2(c).

Fig. 5.Fig. 5. The 10 macromolecules in the simulated dataset used for assisting cryo-ET classification method. In each subfigure, an example of subtomogram slice is shown in left, and the pdb result is shown in the right.

The size of the simulation scene is $300 \ast 300 \ast 300$, the resolution and the voxel size are the same as above. Both the density map compound process and the tomogram generating process can be finished in 5 seconds.

The simulated image describes the scene of a SARS-CoV-2 infecting the host cell. The infection begins when the S-Protein on the virus surface binds to the ACE2 receptors on the cell membrane. The S-Protein is especially crucial, since it is the primary vaccine target exposed on the surface of SARSCoV-2, aiding in the host infection by mediating the binding of virus and host cell receptors and assisting in the fusion of the viral and host cell membranes. Both S-Proteins and ACE2 can be clearly seen in our simulated images and can be traced with their position label. Our proposed approach can automatically generate enough scenes with the virus and the cell membrane, which can be used as a benchmark dataset for testing developing cryo-ET analysis algorithms or as labeled samples to train macromolecule detection and classification framework.

VI.   Assist of Cryo-Et Classification Methods

In order to validate that our data can be used to assist cryo-ET analysis, we generated a dataset containing 15,000 samples, and used it to train and test two cryo-ET classification methods.

A. Dataset

We used three datasets of subtomograms of 32³ voxels. Each dataset had different SNR levels. The SNRs used were 0.03, 0.05 and positive infinity respectively. In each set, we obtained 5000 subtomograms of 10 classes. The 10 types of macromolecules and an example of the corresponding simulated cryo-ET slice could be found in Figure 5.

B. SqueezeNet classification method

The SqueezeNet ^[15] model that is traditionally used for the classification of images and was extended to classify the 3-D subtomograms present in the dataset. We choose the SqueezeNet model because of its high performance on regular computer-vision-based tasks in various domains. The novelty of SqueezeNet lies in the fact that it uses Fire modules. A Fire module essentially applies two different convolutional processes on the same input and concatenates the output. This allows SqueezeNet to attain higher levels of accuracy with a lower number of parameters. The final Dense layer uses a Softmax activation function. This was done in order to obtain the probabilities of the subtomogram pertaining to any of the ten output classes. Adam optimizer was used with a learning rate of 1e-6 along with the categorical cross-entropy loss function.

The adapted SqueezeNet model was trained for 200 epochs until the accuracy on the testing set no longer improved. To aid in the training process, two model callbacks were employed, Model Checkpoint and Reduce Learning Rate on Plateau. The Model Checkpoint would save the best performing model after each epoch and Reduce Learning Rate on Plateau, which was set to a patience value of 10 and a reduction factor of 0.1, would reduce the learning rate by a factor of 0.1 if the accuracy does not improve for 10 consecutive epochs.

The performance of the SqueezeNet model has been tabulated below (see table I). From Table 1 we can infer that the accuracy of the SqueezeNet model is monotonically increasing with the increase in the value of SNR. This intuitively makes sense as with the increase in SNR, the data would essentially become clearer, leading to better prediction accuracy.

C. Convolutional neural network classification method

The aim of our experiment was to successfully classify given data into the ten different categories of protein macromolecules. Convolutional Neural Network (CNN) models are a widely used classification method. It can achieve significantly higher classification accuracy than other rotation invariant feature based methods. Additionally, CNN models scale linearly with respect to the number of inputs, given fixed subtomogram size and class number. Thus, we adapted the CNN architecture particularly by referring to ^[26], a simple CNN architecture which achieved a high accuracy for classification tasks. The CNN architecture consists of two blocks. Each block is comprised of two convolution layers and one max pool layer. The first block uses 32 filters on each convolution layer, whereas the second uses 64 filters on each of the two convolution layers. All convolution layers use ‘ReLU’ activations. These blocks are followed by two fully connected layers of 512 neurons respectively. Finally, the output layer of 10 units uses a ‘Softmax’ activation.

We separated each of the three sets of subtomograms into training and testing sets with ratio 4:1. We used 80% of our data for model fitting and the rest for validation.

In our experiments, we were able to achieve relatively high validation accuracy for all SNR levels. Our results show that lower SNR ratios lead to lower classification accuracy. We see in Table I that the CNN model has achieved the highest accuracy for data with infinite SNR, and the lowest for SNR 0.03.

VII.   Conclusion and Future Work

We proposed an efficient framework for simulating cryo-ET macromolecular crowding. This framework is able to pack a target macromolecule with several random neighbor macromolecules together, and generate the subtomogram for the macromolecule cluster efficiently. The simulated cryo-ET images have pre-specified labels and could be used as benchmark datasets or training and testing datasets for evaluating bioimage analysis methods. We applied the framework to simulate a realistic SARS-CoV-2 infection scene. Our framework packs SARS-CoV-2 constituent proteins together and then placed the host cell membrane with the virus receptor layer next to the virus. This application will potentially aid COVID-19 medical research by enhancing SARS-CoV-2 related bioimage analysis method. We conducted an experiment to classify ten macromolecular protein structures, exposed to three different SNR levels, by two different cryo-ET analysis method (SqueezeNet and CNN). As the signal-to-noise ratio increases, the accuracy of the two models gradually increase, and they produced the highest accuracy of 90.60%.

In the future, we will do more research on macromolecule coarse graining and use multiple-balls to represent one macromolecule. This will obtain a more realistic result with higher crowding level. We will also generate sufficient simulated cryo-ET data and make it public for use by all researchers in this field. At the same time, a benchmark will be performed on the simulated data to evaluate and compare the performance of various cryo-ET methods, so that researchers can choose the appropriate method according to their needs.