Applying Two-Level Simulated Annealing on Bayesian Structure Learning to Infer Genetic Networks

1.   Introduction

Recent high-throughput molecular biology has motivated the development of algorithms and tools for analyzing gene expression data. The central goal is to understand the regulatory mechanism between gene-gene, protein - gene, and protein - protein. Inference of gene networks has been primary focus of research.

There are several gene expression data analysis tools used to reveal the regulatory relations among genes, such as clustering and differential equations. Although clustering algorithms can successfully reveal co-regulated genes, they can not find regulatory relationships ^[2]. At the same time, the detail requirement of relation and parameters of biochemical reactions restrict differential equations to very small systems. Bayesian networks are widely used to infer gene regulatory network from expression data. Bayesian network is a graphical representation of probabilistic relationships between multiple variables. Compared with other methods, Bayesian network is resistant to noise in data, making it more robust for inferring structure. In this paper, we propose an optimization based algorithm to infer the Bayesian network structure. We compare the experimental results with the K2 algorithm based on a Bayesian score value. The results and analysis are provided in section 3.

2.   Method

Inferring Bayesian structure from expression data can be viewed as a search problem in the network space. The goal is to find an optimized network model for the data with maximized/minimized score. Heuristic search algorithms with/without ordering are applied to the structure learning problem because given prior knowledge and the data, the search problem is known to be NP-hard. Simulation annealing is a combinatorial optimization algorithm which is an extension of a Monte Carlo method to determine the equilibrium states of a collection of atoms at any given temperature T ^[1]. It has been proved very successful on solving combinatorial optimization problems including Bayesian structure inferring. The drawback of the algorithm is that after a large number of iterations, the temperature drops to a low degree and the local optimizer reaches its stable state. That means even after applying a perturbation on the optimizer, the new search solution is very likely to fall into the same basin. In such a case, the search will stop at a local optimized solution. In our two-level simulated annealing (TLSA) ^[1], we can solve this optimization problem. The algorithm is described as follows:

Algorithm 1Algorithm 1   two-Level Simulated Annealing

${x_{best}}$ ’ is the optimized solution and ${f_{best}}$ is the best objective function value. ^[1]

In the TLSA, we set up two levels for each candidate x and named them upper level and lower level. The objective function value of lower level for x is the local optimizer value. The perturbation is made on the upper level while the decision on accepting or rejecting the move is depend on the comparison result of lower level objective function values of current and new points. The TLSA could look ahead for the objective function info on local optimizer before making any decision. In the case of low temperature, the TLSA still could work very effectively by accepting better local optimizer without being trapped into certain local optimizer basins.

We can apply TLSA in Bayesian structure learning problem. The x in TLSA algorithm represents a DAG (Directed Acyclic Graph) pattern of Bayesian network. From the decomposition rule in Bayesian network, we can apply Bayesian score equation as the objective function for each variable (gene). $$\eqalignno{& {\rm S}({\rm G}:{\rm D}) = \log{\rm P}({\rm G}\vert {\rm D}) \cr & = \log{\rm P}({\rm D}\vert {\rm G})+\log{\rm P}({\rm G})+{\rm C} \cr & {{\rm S}_{\rm BDe}}={\sum\nolimits_{\rm i}}{{\rm Score}_{\rm BDe}}({\rm Xi},{\rm Pa}({\rm Xi}):D),}$$ where G is the DAG, D is the complete data and Xi is the variable(gene) in the network, Pa(Xi) is the parent set of variable Xi.

The local neighborhood in TLSA could be defined by the operations on the edge between any two nodes in G. The operations between any two nodes are: adding edge, deleting edge and reversing edge. Given certain x which is a network structure, we can apply O(n²) single-step operations in each that will generate x_new in the neighborhood of x. By applying m-step $({\rm m}> 1)$ operations simultaneously, we could move to another disjoint neighborhood for further search.

3.   Results and Conclusion

We applied TLSA algorithm to simulated data set. We build up “Golden Networks” (GNs) with 10 nodes, 20 nodes, 30 nodes and 40 nodes respectively. Simulated data sets are generated from GNs by applying the Monte Carlo Method. We use the resultant sampled data to test Bayesian scores that infer the strength of learning network structures in the design of the TLSA algorithm. The data in each data set has value 0 or 1 which represents down-regulated and up-regulated respectively. In our experiment, the sample size is also fixed. Simulation is run on 10 networks for each kind of GN, the minimized scores are compared with the score we obtained using K2 algorithm. The results are listed in the following graphics:

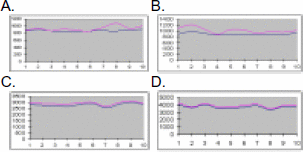
Fig 3.1Fig 3.1

The simulation results show that TLSA can reach better structure with lower score compared with K2 although no ordering information is available in advance. Therefore, TLSA is more likely to find equivalent pattern of the optimized structure from data. Analysis of regulatory networks using other data as well as gene expression data is currently underway.