Provably Secure and Practical Onion Routing

I.   Introduction

Over the last few years the onion routing (OR) network Tor ^[28] has emerged as a successful technology for anonymous web browsing. It currently employs more than two thousand dedicated relays, and serves hundreds of thousands of users across the world. Despite its success, the existing Tor network still lacks a rigorous security analysis, as its security properties have neither been formalized cryptographically nor proven. (See ^{[3],[11],[23]} for previous attempts and their shortcomings.) In this paper, we define security for the third-generation OR protocol Tor, and construct a provably secure and practical OR protocol.

An OR network consists of a set of routers or OR nodes that relay traffic, a large set of users, and directory servers that provide routing information for the OR nodes to the users. A user (say Alice) constructs a circuit by choosing a small sequence of (usually three) OR nodes, where the chosen nodes route Alice's traffic over the path formed. The crucial property of an OR protocol is that a node in a circuit can determine no circuit nodes other than its predecessor and its successor. Alice sends data over the constructed circuit by sending the first OR node a message wrapped in multiple layers of symmetric encryption (one layer per node), called an onion , using symmetric keys agreed upon during an initial circuit construction phase. Consequently, given a public-key infrastructure (PKI), cryptographic challenges in onion routing are to securely agree upon such symmetric keys, and then to use the symmetric keys to achieve confidentiality and integrity.

In the first generation onion routing ^[25], circuits are constructed in a single pass. However, the scalability issues while pursuing forward secrecy ^[7] in the single-pass construction prompted Dingledine, Mathewson and Syverson ^[9] to use a telescoping approach for the next-generation OR protocol Tor. In this telescoping approach, they employed a forward secret, multi-pass key agreement protocol called the Tor authentication protocol (TAP) to negotiate a symmetric session key between user Alice and a node. Goldberg ^[13] presented a security proof for individual instances of TAP. The security of TAP, however, does not automatically imply the security of the Tor protocol. (For a possible concurrent execution attack, see ^[30].) The Tor protocol constitutes a sequential execution of multiple TAP instances as well as onion construction and processing algorithms, and thus its security has to be analyzed in a composability setting.

In this direction, Camenisch and Lysyanskaya ^[3] defined an anonymous message transmission protocol in the universal composability (UC) framework, and presented a protocol construction that satisfies their definition. They motivated their choice of the UC framework for a security definition by its versatility as well as its appropriateness for capturing protocol compositions. However, Feigenbaum, Johnson and Syverson ^[11],[12] observe that the protocol definition presented by Camenisch and Lysyanskaya ^[3] does not correspond to the OR methodology, and a rigorous security analysis of an OR protocol still remains an unsolved problem.

Studies on OR anonymity such as ^{[11],[23],[26]} assume simplified OR black-box models to perform an analysis of the anonymity guarantees of these models. Due to the complexity of an OR network's interaction with the network and the adversary, such black-box models are not trivially realized by deployed OR networks, such as Tor. As a result, there is a gap between deployed OR protocols and anonymity analysis research that has to be filled.

A. Our Contributions

Our contribution is threefold. First, we present a security definition for the OR methodology as an ideal functionality ${\cal F}_{{\rm OR}}$ in the UC framework. This ideal functionality in particular gives appropriate considerations to the goals of various system entities. After that, we identify and characterize which cryptographic primitives constitute central building blocks of onion routing, and we give corresponding security definitions: a one-way authenticated key exchange (1 W-AKE) primitive, and onion construction and processing algorithms. We then describe an OR protocol $\Pi_{{\rm OR}}$ that follows the current Tor specification and that relies on these building blocks as black boxes. We finally show that $\Pi_{{\rm OR}}$ is secure in the DC framework with respect to ${\cal F}_{{\rm OR}}$, provided that these building blocks are instantiated with secure realizations (according to their respective security definitions).

Second, we present a practical OR protocol by instantiating $\Pi_{{\rm OR}}$ with the following OR modules: a 1 W-AKE protocol ntor ^[14], employed onion construction and processing algorithms in Tor with a slightly enhanced integrity mechanism. We show that these instantiations fulfill the security definitions of the individual building blocks that we identified before. This yields the first practical and provably secure OR protocol that follows the Tor specification. As part of these proofs, we identify a novel security definition of symmetric encryption notion we show to be sufficient for showing $\Pi_{{\rm OR}}$ secure. This notion strictly lies between CPA-security and CCA-security and characterizes stateful deterministic countermode encryptions. We call this notion predictably malleable encryptions , which might be of an independent interest.

Third, we illustrate the applicability of the abstraction ${\cal F}_{{\rm OR}}$ by introducing the first cryptographic definition of forward circuit secrecy for onion routing, which might be of independent interest. We utilize the abstraction ${\cal F}_{{\rm OR}}$ and the UC composability theorem for proving that $\Pi_{{\rm OR}}$ satisfies forward circuit secrecy by means of a simple proof. As a second application, we close the gap between the OR black-box model, prevalently used in anonymity analyses ^{[11],[12],[23],[26],} and a cryptographic model $(\Pi_{{\rm OR}})$ of onion routing. Again, we utilize our abstraction ${\cal F}_{{\rm OR}}$ and the UC composability theorem for proving that against local, static attackers the recent analysis of the OR black-box model ^[12] also applies to our OR protocol $\Pi_{{\rm OR}}$ instantiated with secure core building blocks.

Compared to previous work ^[3], we construct an OR circuit interactively in multiple passes, whereas previous work did not consider circuit construction at all, and hence does not model the widely used Tor protocol. The previous approach, and even single-pass circuit construction in general, restricts the protocol to eventual forward secrecy, while a multi-pass circuit construction ensures forward secrecy immediately after the circuit is closed. Second, we show that their hop-to-hop integrity verification is not mandatory, and that an end-to-end integrity verification suffices for onion routing. Finally, they do not consider backward messages (from web-servers to Alice), and their onion wrapping and unwrapping algorithms also do not work in the backward direction.

There has also been work on universally composable Mix-Nets by Wikström ^[29]. That work has some similarities to our work, but it only considers Mix-Nets, e.g., it does not need to cope with circuits and sessions.

Another important approach for analyzing onion routing has been conducted by Feigenbaum, Johnson, and Syverson ^[10]. In contrast to our work, the authors analyze an I/O automaton that use idealized encryption, pre-shared keys, and assume that every party only constructs one circuit to one destination. Moreover, the result in that work only holds in the stand-alone model against a local attackers whereas our result holds in the UC model against global and partially global attackers. In particular, by the UC composability theorem our result even holds with arbitrary protocols surrounding and against an attacker that controls parts of the network.

Outline of the Paper . Section II provides background information relevant to onion routing, 1 W-AKE, and the DC framework. Section III, presents our security definition for onion routing. Section IV, presents cryptographic definitions for predictably malleable encryptions and secure onion construction and processing algorithms. Section V, states that given a set of secure OR modules we can construct a secure OR protocol. Section VII utilizes our security definition to analyze some security and anonymity properties of onion routing. Finally, we discuss some further interesting directions in Section VIII. In this work, many proofs have been omitted due to space constraints, which can be found in the full version ^[1].

II.   Background

In this paper, we often omit the security parameter $\kappa$ when calling an algorithm $A$; i.e., we abbreviate $A(1^{\kappa}, x)$ by $A(x)$. We write $y\leftarrow A(x)$ for the assignment of the result of $A(x)$ to a variable $y$, and we write $y\,\displaystyle\mathop{\leftarrow}^{\$}\,S$ for the assignment of a uniformly chosen element from $S$ to $y$ For a given security parameter $\kappa$, we assume a message space $M(\kappa)$ that is disjoint from the set of onions. We assume a distinguished error message $\perp$; in particular, $\perp$ is not in the message space. For some algorithms, we write $Alg(\alpha, b, c, [d])$ and mean that the argument $d$ is optional. Finally, for stateful algorithms, we write $y\leftarrow A(x)$ but we actually mean $(y,s^{\prime})\rightarrow A(x,s)$, where $s^{\prime}$ is used in the next invocation of $A$ as a state, and $s$ is the stored state from the previous invocation. We assume that for all algorithms $s\in\{0,1^{\kappa}\}$.

A. Onion Routing Circuit Construction

In the original Onion Routing project ^{[16],[17],[25],[27],} circuits were constructed in a single pass. However, such a single-pass circuit construction does not provide forward secrecy : if an adversary corrupts a node and obtains the private key, the adversary can decrypt all of the node's past communication. Although changing the public/private key pairs for all OR nodes after a predefined interval is a possible solution (eventual forward secrecy), this solution does not scale to realistic OR networks such as Tor, since at the start of each interval every user has to download a new set of public keys for all the nodes.

Pairing-based onion routing (PB-OR) ^[21] and certificate-less onion routing (CL-OR) ^[6] attempt to provide better single-pass constructions. However, both approaches do not yield satisfactory solutions: CL-OR suffers from the same scalability issues as the original OR protocol ^[20]; PB-OR requires a distributed private-key generator ^[19] that may lead to inefficiency in practice.

Another problem with the single-pass approach is its intrinsic restriction to eventual forward secrecy ^[22]; i.e., if the current private key is leaked, then past sessions remain secret only if their public and private keys have expired. A desirable property is that all past sessions that are closed remain secret even if the private key is leaked; such a property is called immediate forward secrecy.

In the current Tor protocol, circuits are constructed using a multi-pass approach that is based on TAP. The idea is to use the private key only for establishing a temporary session key in a key exchange protocol. Together with the private key, additional temporary (random) values are used for establishing the key such that knowing the private key does not suffice for reconstructing the session key. These temporary values are erased immediately after the session key has been computed. This technique achieves immediate forward secrecy in multi-pass constructions, which however was never formallv defined or proven before.

The multi-pass approach incurs additional communication overhead. However, in practice, almost all Tor circuits are constructed for a circuit length of $\ell=3$, which merely causes an overhead of six additional messages. With this small overhead, the multi-pass circuit construction is the preferred choice in practice, due to its improved forward secrecy guarantees. Consequently, for our OR security definition we consider a multi-pass circuit construction as in Tor.

B. One-Way Authenticated Key Exchange - 1W-AKE

In a multi-pass circuit construction, a session key is established via a Diffie-Hellman key exchange. However, the precise properties required of this protocol were not formalized until recently. Goldberg, Stebila and Ustaoglu ^[14] formalized the concept of 1 W-AKE, presented an efficient instantiation, and described its utility towards onion routing. We review their work here and we refer the readers to ^[14] for a detailed description.

An authenticated key exchange (AKE) protocol establishes an authenticated and confidential communication channel between two parties. Although AKE protocols in general aim for key secrecy and mutual authentication, there are many practical scenarios such as onion routing where mutual authentication is undesirable. In such scenarios, two parties establish a private shared session key, but only one party authenticates to the other. In fact, as in Tor, the unauthenticated party may even want to preserve its anonymity. Their 1 W-AKE protocol constitutes this precise primitive.

The 1W-AKE protocol consists of three procedures: Initiate, Respond , and ComputeKey . With procedure Initiate , Alice (or her onion proxy) generates and sends an authentication challenge to the server (an OR node). The OR node responds to the challenge by running the Respond procedure, and returning the authentication response. The onion proxy (OP) then runs the ComputeKey procedure over the received response to authenticate the OR node and compute the session key.

The security of a 1W-AKE is defined by means of a challenger that represents all honest parties. The attacker is then allowed to query this challenger. If the attacker is not able to distinguish a fresh session key from a randomly chosen session key, we say that the 1 W-AKE is secure . This challenger is constructed in a way that security of the 1 W-AKE implies one-way authentication of the responding party.

For the definition of one-way anonymity we introduce a proxy, called the anonymity challenger, that relays all messages from and to the usual 1 W-AKE challenger except for a challenge party $C$. The attacker can choose two challenge parties, out of which the anonymity challenger randomly picks one, say $i^{\ast}$. Then, the anonymity challenger relays all messages that are sent to $C$ to $P_{i^{\ast}}$ (via the 1 W-AKE challenger).

In the one-way anonymity experiment, the adversary can issue the following queries to the challenger $C$. All other queries are simply relayed to the 1W-AKE challenger. The session $\Psi^{ }$ denotes the challenge session. The two queries are for activation and communication during the test session. We say that a 1 W-AKE is one-way anonymous if the attacker cannot guess which party has been guessed with more than $1/2+\mu(\kappa)$ probability, where $\mu$ is a negligible function.

In terms of instantiation, Goldberg et al. showed that an AKE protocol suggested for Tor—the fourth protocol in ^[24]—can be attacked, leading to an adversary determining all of the user's session keys. They then fixed the protocol (see Figure 13) and proved that the fixed protocol (ntor) satisfies the formal properties of 1 W-AKE. In our OR analysis, we use their formal definition and their fixed protocol.

C. The UC Framework: an Overview

The UC framework is designed to enable a modular analysis of security protocols. In this framework, the security of a protocol is defined by comparing it with a setting in which all parties have a direct and private connection to a trusted machine that computes the desired functionality. As an example consider an authenticated channel between Alice and Bob with a passive attacker. In the real world Alice would call a protocol that signs the message $m$ to be communicated and sends the signed message over the network such that Bob would verify the signature. In the setting with a trusted machine $T$, however, Alice sends the message $m$ directly to $T;\,T$ notifies the attacker about $m$, and $T$ directly sends $m$ to Bob. This trusted machine is called the ideal functionality .

Security in the UC framework is defined as follows: a protocol $\pi$UC-realizes an ideal functionality ${\cal F}$ if for all probabilistic poly-time (PPT) attackers ${\cal A}$ there is a PPT simulator $S$ such that no PPT machine can distinguish an interaction with $\pi$ and ${\cal A}$ from an interaction with ${\cal F}$ and $S$. The distinguisher is connected to the protocol and the attacker (or the simulator).

In contrast to typical UC proofs, our attacker model considers a more fine-grained network topology. Typically, a global attacker is assumed in UC; however, as we also want to be able to argue about local attackers, we prove our result for partially global attackers, i.e., in particular also for completely global attackers. A network over which the attacker does not have full control is modelled by a network functionality ${\cal F}_{{\rm NET}^{q}}$ in which the attacker can adaptively compromise up to $q$ links between honest onion routers. This network functionality is a global setup assumption; consequently, we have to consider the generalized UC framework (GUC) by Canetti, Dodis, Pass, and Walfish ^[5]. Throughout this work, if we say that a protocol $\rho$ UC realizes a protocol $\pi$ we actually mean that $\rho^{GUC}$ realizes $\pi$. (For a thorough definition of GUC, we refer to ^[5].)

D. The OR Protocol

We describe an OR protocol $\Pi_{{\rm OR}}$ that follows the Tor specification ^[8]. We do not present the cryptographic algorithms, e.g., wrapping and unwrapping onions, in this section but only present the skeleton of the protocol. A thorough characterization of these cryptographic algorithms follows in Section IV.

We describe our protocols using pseudocode and assume that a node maintains a state for every execution and responds (changes the state and/or sends a message) upon receiving a message as per its current state. In Figure 1, we give an overview of the setup that we consider.

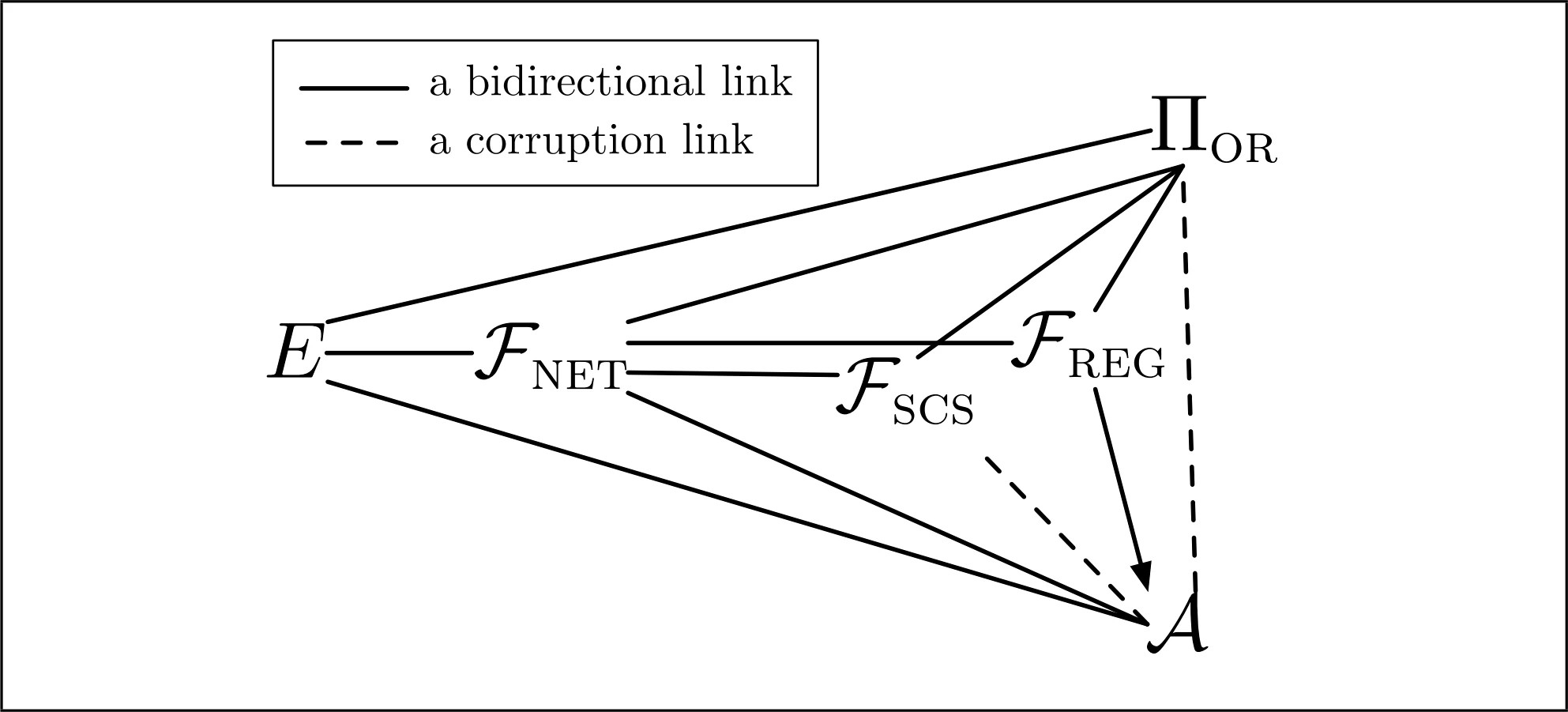
Figure 1.Figure 1.

As an attacker model we consider a partially global attacker in contrast to the global attacker that is typically used in UC analyses. For modelling a partially global attacker, we introduce an ideal functionality ${\cal F}_{{\rm NET}^{q}}$ that allows the attacker to compromise at most $q$ links.

There are two types of messages that the protocol generates and processes: the first type contains input actions , which carry inputs to the protocol from the user (Alice), and output actions , which carry outputs of the protocol to Alice. The second message type is a point-to-point network message (a cell in the OR literature), which is to be delivered by one protocol node to another. To enter a wait state, a thread may execute a command of the form wait for a network message.

With this methodology, we are able to effortlessly extract an OR protocol $(\Pi_{{\rm OR}})$ from the Tor specification by categorizing actions based on the OR cell types (see Figure 2). For ease of exposition, we only consider Tor cells that are cryptographically important and relevant from the security definitional perspective. In particular, we consider create, created and destroy cells among control cells, and data, extend and extended cells among relay cells. We also include two input messages cc and send, where Alice uses cc to create OR circuits and uses send to send messages $m$ over already-created circuits. We do not consider streams and the SOCKS interface in Tor as they are extraneous to the basic OR methodology. We unify instructions for an OP (onion proxy) node and an OR node for the simplicity of discussion. Moreover, for the sake of brevity, we restrict ourselves to messages $m\in M(\kappa)$ that fit exactly in one cell. It is straight-forward to extend our result to a protocol that accepts larger messages. The only difference is that the onion proxy and the exit node divide messages into smaller pieces and recombine them in an appropriate way.

Figure 2.Figure 2.

Function calls Initiate, Respond and ComputeKey correspond to 1 W-AKE function calls described in Section II-B. Function calls $WrOn$ and UnwrOn correspond to the principal onion algorithms. $WrOn$ creates a layered encryption of a payload (plaintext or onion) for given an ordered list of $\ell$ session keys for $\ell\geq 1$UnwrOn removes $\ell$ layers of encryptions from an onion to output a plaintext or an onion given an input onion and a ordered list of $\ell$ session keys for $\ell\geq 1$. Moreover, onion algorithms also ensure endto-end integrity. The cryptographic requirements for these onion algorithms are presented in Section IV-B.

Tor uses a centralized approach to determine valid OR nodes and distribute their public keys. Every OR node has to be registered in so-called directory servers, where each registration is checked by an administrator. These directory servers then distribute the list of valid OR nodes and the respective public keys. We abstract the key registration procedure by assuming that the directory servers expect a fixed set of parties upon setup. Formally, we model these directory servers as an ideal functionality ${\cal F}_{{\rm RFC}}^{\cal N}$, which is basically defined as by Canetti ^[4] except that ${\cal F}_{{\rm REG}}^{\cal N}$ rejects all parties that are not in ${\cal N}$ and only sends the public keys around once all parties in ${\cal N}$ registered. Tor does not guarantee any anonymity once these directory servers are compromised. Therefore, we concentrate on the case in which these directory servers cannot be compromised. As in Tor, we assume that the list of valid OR nodes is given to the directory servers from outside, in our case from the environment. However, for the sake of simplicity we assume that the OR list is only synchronized initially. In detail, we slightly extend the functionality as follows. ${\cal F}_{{\rm RFC}}^{\cal N}$ initially receives a list of OR nodes from the environment, waits for each of these parties for a public key, and distributes the list of OR nodes and their public keys as (registered, $\langle P_{j}, pk_{j}\rangle_{j=1}^{n}$) . Each OR node, on the other hand, initially computes its long-term keys ($sk, pk$) and registers the public part at ${\cal F}_{{\rm REG}}^{\cal N}$. Then, the node waits to receive the message (registered, $\langle P_{j}, pk_{j}\rangle_{j=1}^{n}$) from ${\cal F}_{{\rm REG}}^{\cal N}$ before declaring that it is ready for use.

OPs develop circuits incrementally, one hop at a time, using the ExtendCircuit function defined in Figure 3. To create a new circuit, an OP sends a create cell to the first node, after calling the Initiate function of 1 W-AKE; the first node responds with a created cell after running the Respond function. The OP then runs the ComputeKey function. To extend a circuit past the first node, the OP sends an extend relay cell after calling the Initiate function, which instructs the last node in the circuit to send a create cell to extend the circuit.

Figure 3.Figure 3.

Circuits are identified by circuit IDs ($cid\in\{0,1\}^{\kappa}$) that associate two consecutive circuit nodes. We denote circuit at a node $P_{i}$ using the terminology ${\cal C}=P_{i-1}\displaystyle\mathop{\Leftrightarrow}^{cid_{i},k_{i}}P_{i}\displaystyle\mathop{\Leftrightarrow}^{cid_{i+1}}$$P_{i+1}$, which says that $P_{i-1}$ and $P_{i+1}$ are respectively the predecessor and successor of $P_{i}$ in a circuit ${\cal C}$. $k_{i}$ is a session key between $P_{i}$ and the OP, while the absence of $k_{i+1}$ indicates that a session key between $P_{i+1}$ and the OP is not known to $P_{i}$; analogously the absence of a circuit id $cid$ in that notation means that only the first circuit id is known, as for OP, for example. Functions prev and next on $cid$ correspondingly return information about the predecessor or successor of the current node with respect to $cid$; e.g., next $(cid_{i})$ returns $(P_{i+1},\, cid_{i+1})$ and next $(cid_{i+1})$ returns $\perp$, The OP passes on to Alice $\langle p \displaystyle\mathop{\Leftrightarrow}^{cid_{1}}P_{1}\Leftrightarrow\cdots P_{\ell}\rangle$.

Within a circuit, the OP and the exit node use relay cells created using WrOn to tunnel end-to-end commands and connections. The exit nodes use some additional mechanisms (abstracting the streams used in Tor) to synchronize communication between the network and a circuit ${\cal C}$. We represent that using sid . With this auxiliary synchronization, end-to-end communication between OP and the exit node happens with a WrOn call with multiple session keys and a series of UnwrOn calls with individual session keys in the forward direction, and a series of WrOn calls with individual session keys, and finally a UnwrOn call with multiple session keys in the backward direction. Communication in the forward direction is initiated by a send message by Alice to the OP, while communication in the backward direction is initiated by a network message to the exit node. Cells are exchanged between OR nodes over a secure and authenticated channels, e.g., a TLS connection. We abstract such a channel in the UC framework by a functionality ${\cal F}_{{\rm scs}}$ as proposed by Canetti ^[4] with the only difference that ${\cal F}_{{\rm scs}}$ does not output the leakage to the attacker but to ${\cal F}_{{\rm NET}^{q}}$, i.e., the network functionality. We write $storeX\leftarrow v$ for either introducing a new variable $X$ with value $v$, or assign a value $v$ to a variable $X$ in case $X$ was not previously defined.

To tear down a circuit completely, an OR or OP sends a destroy cell to the adjacent nodes on that circuit with appropriate $cid$ using the DestroyCircuit function defined in Figure 3. Upon receiving an outgoing destroy cell, a node frees resources associated with the corresponding circuit. If it is not the end of the circuit, it sends a destroy cell to the next node in the circuit. Once a destroy cell has been processed, the node ignores all cells for the corresponding circuit. Note that if an integrity check fails during UnwrOn , the destroy cells are sent in the forward and backward directions in a similar way.

In the Tor the OP has a time limit (of ten minutes) for each established circuit; thereafter, the OP constructs a new circuit. However, the UC framework does not provide a notion of time. We model such a time limit in the UC framework by only allowing a circuit to transport at most a constant number (say ttl_C) of messages measured using the used function call. Afterwards, the OP discards the circuit and establishes a fresh circuit.

E. An OR Black Box Model

Anonymity in a low-latency OR network does not only depend upon the security of the onions but also upon the magnitudes and distributions of users and their destination servers. In the OR literature, considerable efforts have been put towards measuring the anonymity of onion routing ^{[10][11][12],[23],[26]}.

Feigenbaum, Johnson, and Syverson used for an analysis of the anonymity properties of onion routing an ideal functionality $B_{{\rm OR}}\,[12]$. This functionality emulates an I/O automata model for onion routing from ^[10],[11]. Figure 4 presents this functionality ${\cal B}_{\rm OR}$.

Figure 4.Figure 4.

Let ${\rm N}_{{\rm OR}}$ be the set of onion routers, and let ${\rm N}_{\cal A}$ of those be eavesdropped, where $b=\vert {\rm N}_{{\cal A}}\vert /\vert {\rm N}_{{\rm OR}}\vert$ defines the fraction of compromised nodes. It takes as input from each user $U$ the identity of a destination $S$, For every such connection between a user and a destination, the functionality may reveal to the adversary the identity of the user (sent, $U$ –) (i.e., the first OR router is compromised), the identity of the destination (sent, –, $S, [m]$) (i.e., the exit node is compromised), both (sent, $U, S, [m]$) (i.e., the first OR router and the exit node are compromised) or only a notification that something has been sent (sent,–, –) (i.e., neither the first OR router nor the exit node is compromised).

We stress that this functionality only abstracts an OR network against local attackers. As the distribution of the four cases only depends on the first and the last router being compromised but not on the probability that the attacker controls sensitive links between honest parties, ${\cal B}_{{\rm OR}}$ only models OR against local adversaries. As an example consider, the case in which the attacker only wiretaps the connection between the exit node and the server. In this case, the attacker is able to determine which message has been sent to whom, i.e., the abstraction needs to leak (sent, –, $S, [m]$); however, the probability of this event is $c$, where $c$ is the fraction of observed links between honest onion routers and users and servers. Therefore, ${\cal B}_{{\rm OR}}$ cannot be used as an abstraction for onion routing against partially global attackers.

We actually present ${\cal B}_{{\rm OR}}$ in two variants. In the first variant ${\cal B}_{{\rm OR}}$ does not send an actual message but only a notification. This variant has been analyzed by Feigenbaum, Johnson, and Syverson. We additionally consider the variant in which ${\cal B}_{{\rm OR}}$ sends a proper message $m$. We denote these two variants by marking the message $m$ as optional, i.e., as $[m]$.

In order to justify these OR anonymity analyses that consider an OR network as a black box, it is important to ascertain that these black boxes indeed model onion routing. In particular, it is important under which adversary and network assumptions these black boxes model and securely abstract real-world OR networks. In this work, we show that the black box ${\cal B}_{{\rm OR}}$ can be UC-realized by a simplified version of the Tor network.

III.   Security Definition of OR

In this section, we first describe our system and adversary model for all protocols that we analyze (Section III-A). Thereafter, we present a composable security definition of OR by introducing an ideal functionality (abstraction) ${\cal F}_{{\rm OR}}$ in the UC framework (Section III-B).

Tor was designed to guarantee anonymity even against partially global attackers, i.e., attackers that do not only control compromised OR nodes but also a portion of the network. Previous work, however, only analyzed local, static attackers ^{[10][11][12],} such as the abstraction ${\cal B}_{{\rm OR}}$ presented in Figure 4. In contrast, we analyze onion routing against partially global attackers. As our resulting abstraction ${\cal F}_{{\rm OR}}$ has to faithfully reflect that an active attacker can hold back all onions that it observes, ${\cal F}_{{\rm OR}}$ is naturally more complex than ${\cal B}_{{\rm OR}}$.

A. System and Adversary Model

We consider a fully connected network of $n$ parties ${\rm N}=\{P_{1}, \ldots, P_{n}\}$. For simplicity of presentation, we consider all parties to be OR nodes that also can function as OPs to create circuits and send messages. It is also possible to use our formulation to model separate user OPs that only send and receive messages but do not relay onions.

Tor has not been designed to resist against global attackers. Such an attacker is too strong for many practical purposes as it can simply break the anonymity of an OR protocol by holding back all but one onion and tracing that one onion though the network. However, in contrast to previous work, we do not only consider local attackers, which do not control more than the compromised OR routers, but also partially global attackers that control a certain portion of the network. Analogous to the network functionality ${\cal F}_{{\rm SYN}}$ proposed by Canetti ^[4], we model the network as an ideal functionality ${\cal F}_{{\rm NET}^{q}}$, which bounds the number of attacker-controlled links to $q\in[0, {n\choose 2}]$. For attacker-controlled links the messages are forwarded to the attacker; otherwise, they are directly delivered. In Section VII we show that previous black-box analyses of onion routing against local attackers applies to our setting as well by choosing $q:=0$. Let ${\rm s}$ represent all possible destination servers $\{S_{1}, \ldots, S_{\Delta}]$ which reside in the network abstracted by a network functionality ${\cal F}_{{\rm NFT}^{q}}$.

We stress that the UC framework does not provide a notion of time; hence, the analysis of timing attacks, such as traffic analysis, is not in the scope of this work.

Adaptive Corruptions . Forward secrecy ^[7] is an important property for onion routing. In order to analyze this property, we allow adaptive corruptions of nodes by the attacker ${\cal A}$. Such an adaptive corruption is formalized by a message compromise, which is sent to the respective party. Upon such a compromise message the internal state of that party is deleted and a long-term secret key $sk$ for the node is revealed to the attacker. ${\cal A}$ can then impersonate the node in the future; however, ${\cal A}$ cannot obtain the information about its ongoing sessions. We note that this restriction arises due to the currently available security proof techniques and the well-known selective opening problem with symmetric encryptions ^[18], and the restriction is not specific to our constructions ^[2],[15]. We could also restrict ourselves to a static adversary as in previous work ^[3]; however, that would make an analysis of forward secrecy impossible.

B. Ideal Functionality

The presentation of the ideal functionality ${\cal F}_{{\rm OR}}$ is along the lines of the description OR protocol $\Pi_{{\rm OR}}$ from Section II-D. We continue to use the message-based state transitions from $\Pi_{{\rm OR}}$, and consider sub-machines for all $n$ nodes in the ideal functionality. To communicate with each other through messages and data structures, these sub-machines share a memory space in the functionality. The sub-machine pseudocode for the ideal functionality appears in Figure 5 and three subroutines are defined in Figure 6. As the similarity between pseudocodes for the OR protocol and the ideal functionality is obvious, rather than explaining the OR message flows again, we concentrate on the differences.

Figure 5.Figure 5.

Figure 6.Figure 6.

The only major difference between $\Pi_{{\rm OR}}$ and ${\cal F}_{{\rm OR}}$ is that cryptographic primitives such as message wrapping, unwrapping, and key exchange are absent in the ideal world; we do not have any keys in ${\cal F}_{{\rm OR}}$, and the OR messages WrOn and UnwrOn as well as the 1 W-AKE messages Initiate, Respond , and ComputeKey are absent.

The ideal functionality also abstracts the directory server and expects on the input/output interface of ${\cal F}_{{\rm REG}}^{\cal N}$ (from the setting with $\Pi_{{\rm OR}}$) an initial message with the list $\langle P_{i}\rangle_{i=1}^{n}$ of valid nodes. This initial message corresponds to the list of onion routers that have been approved by an administrator. We call the part of ${\cal F}_{{\rm oR}}$ that abstracts the directory servers dir. For the sake of brevity, we do not present the pseudocode of dir. Upon an initial message with a list $\langle P_{i}\langle_{i=1}^{n}$ of valid nodes, dir waits for all nodes $P_{i}(i\,\in\,\{1, \ldots, n\})$ for a message (register, $P_{i}$). Once all nodes registered, dir sends a message (registered, $\langle P_{i}\rangle_{i=1}^{n}$) with a list of valid and registered nodes to every party that registered, and to every party that sends a retrieve message to dir.

Messages from ${\cal A}$and ${\cal F}_{{\rm NET}^{q}}$. In Figure 5 and Figure 7, we present the pseudocode for the attacker messages and the network functionality, respectively. For our basic analysis, we model an adversary that can control all communication links and servers in ${\cal F}_{{\rm NFT}^{q}}$, but cannot view or modify messages between parties due to the presence of the secure and authenticated channel. Therefore, sub-machines in the functionality store their messages in the shared memory, and create and send handles $\langle P, P_{next}, h\rangle$ for these messages ${\cal F}_{{\rm NET}^{q}}$. The message length does not need to be leaked as we assume a fixed message size (for all $M(\kappa)$) . Here, $P$ is the sender, $P_{next}$ is the receiver and $h$ is a handle or a pointer to the message in the shared memory of the ideal functionality. In our analysis, all ${\cal F}_{{\rm NET}^{q}}$ messages flow to ${\cal A}$ which may choose to return these handles back to ${\cal F}_{{\rm OR}}$ through ${\cal F}_{{\rm NET}^{q}}$ at its own discretion. However, ${\cal F}_{{\rm NET}^{q}}$ also maintains a mechanism through observedLink flags for the non-global adversary ${\cal A}$. The adversary may also corrupt or replay the corresponding messages; however, these active attacks are always detected by the receiver due to the presence of a secure and authenticated channel between any two communicating parties and we need not model these corruptions.

Figure 7.Figure 7.

The adversary can compromise a party $P$ or server $S$ by sending a compromise message to respectively ${\cal F}_{{\rm OR}}$ and ${\cal F}_{{\rm NET}^{q}}$. For party $P$ or server $S$, the respective functionality then sets the compromised tag to true . Furthermore, all input or network messages that are supposed to be visible to the compromised entity are forwarded to the adversary. In principle, the adversary runs that entity for the rest of the protocol and can send messages from that entity. In that case, it can also propagate corrupted messages which in $\Pi_{{\rm OR}}$ can only be detected during Unun On calls at OP or the exit node. We model these corruptions using corrupted $(msg)=$ { true, false} status flags, where corrupted (msg) status of messages is maintained across nodes until they reach end nodes. Furthermore, for every corrupted message, the adversary also provides a modification function $T(\cdot)$ as the end nodes run by the adversary may continue execution even after observing a corrupted flag. In that case, $T(\cdot)$ captures the exact modificaiton made by the adversary.

We stress that ${\cal F}_{{\rm OR}}$ does not need to reflect reroutings and circuit establishments initiated by the attacker, because the attacker learns, loosely speaking, no new information by rerouting onions. Similar to the previous work ^[3], a message is directly given to the adversary if all remaining nodes in a communication path are under adversary control.

IV.   Secure OR Modules

We identify the core cryptographic primitives for a secure OR protocol. In this section, we present a cryptographic characterization of these core cryptographic primitives which we call secure OR modules . Secure OR modules consist of two parts: first, secure onion algorithm, and second, a one-way authenticated key exchange primitive (lW-AKE), a notion recently introduced by Goldberg, Stebila, and Ustaoglu ^[14].

Onion algorithms typically use several layers of encryptions and possibly integrity mechanisms, such as message authentication codes. Previous attempts ^[3] for proving the security OR protocols use mechanisms to ensure hop-to-hop integrity, such as non-malleable encryption schemes. The widely-used Tor network, however, does not use hop-to-hop integrity but only end-to-end integrity. In the analysis of OR protocols with only end-to-end integrity guarantees, we also have to consider the cases in which the end node is compromised, thus no integrity check is performed at all. In order to cope with these cases, we identify a new notion of predictably malleable encryption schemes. Predictable malleability allows the attacker to change the ciphertexts but requires the resulting changes to the plaintext to be efficiently predictable given only the changes of the ciphertext. In Section IV-A we rigorously define the notion of predictably malleable encryption schemes.

Inspired by Section IV-A, we introduce in Section IV-B the notion of secure onion algorithms .

In the following definitions, we assume the PPT machines to actually be oracle machines. We write $A^{B}$ to denote that $A$ has oracle access to $B$.

A. Predictably Malleable Encryption

Simulation-based proofs often face their limits when dealing with malleable encryption schemes. The underlying problem is that malleability induces an essentially arbitrarily large number of possibilities to modify ciphertexts, and the simulator has no possibility to predict the resulting changes to the corresponding plaintext.

We characterize the property of predicting the changes to the plaintext merely given the modifications on the ciphertext. Along the lines of the IND-CCA definition for stateful encryption schemes, we define the notion of predictably malleable (IND-PM) encryption schemes. The attacker has access to an encryption and a decryption oracle, and either all encryption and decryption queries are honestly answered (the honest game) or all are faked (the faking game), i.e., $0^{\vert m\vert}$ is encrypted instead of a message $m$. In the faking game, the real messages are stored in some shared datastructure $q$, and upon a decryption query only look-ups in $q$ are performed. The IND-PM challenger maintains a separate state, e.g., a counter, for encryption and decryption. These respective states are updated with each encryption decryption query.

In contrast to the IND-CCA challenger, the IND-PM challenger (see Figure 8) additionally stores the produced ciphertext together with the corresponding plaintext for each encryption query. Moreover, for each decryption call the challenger looks up the stored ciphertexts and messages. The honest decryption ignores the stored values and performs an honest decryption, but the faking decryption compares the stored ciphertext with the ciphertext from the query and tries to predict the modifications to the plaintext. Therefore, we require the existence of an efficiently computable algorithm M that outputs the description of an efficient transformation procedure $T$ for the plaintext given the original ciphertext as well as the modified ciphertext.

Figure 8.Figure 8.

B. Secure Onion Algorithms

We identify the onion wrapping (WrOn) and unwrapping (UnwrOn) algorithms as central building blocks in onion routing. We identify four core properties of onion algorithms. The first property is correctness , i.e., if all parties behave honestly, the result is correct. The second property is the security of statefulness, coined synchronicity . It roughly states that whenever a wrapping and an unwrapping algorithms are applied to a message with unsynchronous states, the output is completely random. The third property is end–to-end integrity . The fourth property states that for all modifications to an onion the resulting changes in the ciphertext are predictable. We this property predictable malleability .

Onion Correctness

The first property of secure onion algorithms is onion correctness . It states that honest wrapping and unwrapping results in the same message. Moreover, the correctness states that whenever the unwrapping algorithm has a fake flag, it does not care about integrity, because for $m\in M(\kappa)$ the integrity measure is always added, as required by the end-to-end integrity. But for $m\not\in M(\kappa)$ but of the right length, the wrapping is performed without an integrity measure. The fake flag then causes the unwrapping to ignore the missing integrity measure. Then, we also require that the state transition is independent from the message or the key.

Synchronicity

The second property is synchronicity. In order to achieve replay resistance, we have to require that once the wrapping and unwrapping do not have synchronized states anymore, the output of the wrapping and unwrapping algorithms is indistinguishable from randomness.

End-to-end integrity

The third property that we require is end-to-end integrity; i.e., the attacker is not able to produce an onion that successfully unwraps unless it compromises the exit node. For the following definition, we modify ${\rm OS}\hbox{-}{\rm Ch}^{0}$ such that, along with the output of the attacker, also the state of the challenger is output. In turn, the resulting challenger ${\rm OS}\hbox{-}{\rm Ch}^{0^{\prime}}$ can optionally get a state $s$ as input. In particular, $(a, s)\leftarrow A^{B}$ denotes in the following definition the pair of the outputs of $A$ and $B$.

For the following definition we use the modified challenger ${\rm OS}\hbox{-}{\rm Ch}^{0^{\prime}}$, which results from modifying ${\rm OS}\hbox{-}{\rm Ch}^{0}$ such that along with the output of the attacker also the state of the challenger is output. The resulting challenger ${\rm OS}\hbox{-}{\rm Ch}^{0^{\prime}}$ can, moreover, optionally get a state $s$ as input.

Definition 4

(End-to-end integrity):

Let $S(O, cid)$ be the machine that sends a (destruct, $O$) query to the challenger and outputs the response. Let $Q^{\prime}(s)$ be the set of answers to construct queries from the challenger to the attacker. Let the last onion $O_{\ell^{\prime}}$ of an onion $O_{1}$ be defined as follows: $$\eqalignno{ &{\rm Last} (O_{1}):\cr &\quad{\bf for}\ i= 1\ {\rm to} \ell^{\prime}-1\ {\bf do}\cr &\qquad O_{i+1}\leftarrow UnwrOn(O_{i})}$$

Let $Q(s):=\{$ Last $(O_{1})\mid O_{1}\in Q^{\prime}(s)\}$ be the set of last onions answers to the challenger. We say a set of onion algorithms has end-to-end integrity if for all PPT attackers ${\cal A}$ the following is negligible in $\kappa$ $$\eqalignno{ &{\rm Pr}[(O, s)\leftarrow {\cal A}(1^{\kappa})^{{\rm OS}-{\rm Ch}^{0^{\prime}}}, (m, s^{\prime})\leftarrow S(O, cid)^{{\rm OS}-{\rm Ch}^{{\rm O}^{\prime}}(s)}\cr &\qquad: m\in M(\kappa)\wedge P_{\ell^{\prime}}\ {\rm is \ honest} \wedge O\not\in Q(s^{\prime})].}$$

Predictably Malleable Onion Secrecy .

The fourth property that we require is predictably malleable onion secrecy , i.e., for every modification to a ciphertext the challenger is able to compute the resulting changes for the plaintext. This even has to hold for faked plaintexts.

In detail, we define a challenger ${\rm OS}\hbox{-}{\rm Ch}^{0}$ that provides, a wrapping, a unwrapping and a send and a destruct oracle. In other words, the challenger provides the same oracles as in the onion routing protocol except that the challenger only provides one single session. We additionally define a faking challenger ${\rm OS}\hbox{-}{\rm C}^{1}$ that provides the same oracles but fakes all onions for which the attacker does not control the final node.

For ${\rm OS}\hbox{-}{\rm Ch}^{1}$, we define the maximal paths that the attacker knows from the circuit. A visible subpath of a circuit $(P_{i}, k_{i}, cid_{i})_{i=1}^{\ell}$ from an honest onion proxy is a minimal subsequence of corrupted parties $(P_{i})_{i=u}^{s}$ of $(P_{i})_{i=1}^{\ell}$ such that $P_{i-1}$ is honest and either $s=\ell$ or $P_{s+1}$ is honest as well. The parties $P_{i-1}$ and, if existent, $P_{s+1}$ are called the guards of the visible subpath $(P_{i})_{i=u}^{s}$. We store visible subpaths by the first $cid=cid_{u}$.

Figure 9 and 10 presents ${\rm OS}\hbox{-}{\rm Ch}^{0}$, and ${\rm OS}\hbox{-}{\rm Ch}^{1}$, respectively.

Figure 9.Figure 9.

Figure 10.Figure 10.

V. $\Pi_{\rm OR}$ UC-Realizes${\cal F}_{\rm OR}$

In this section, we show that $\Pi_{{\rm OR}}$ can be securely abstracted as the ideal functionality ${\cal F}_{{\rm OR}}$.

Recall that $\pi$ securely realizes ${\cal F}$ in the ${\cal F}^{\prime}$'-hybrid model if each party in the protocol $\pi$ has a direct connection to ${\cal F}^{\prime}$. ${\cal F}_{{\rm REG}}^{\cal N}$ is the key registration, ${\cal F}_{{\rm SCS}}$ is the secure channel functionality, and ${\cal F}_{{\rm NET}^{q}}$ is the network functionality, where $q$ is the upper bound on the corruptable parties. We prove our result in the ${\cal F}_{{\rm REG}}^{\cal N},\, {\cal F}_{{\rm SCS}}$-hybrid model; i.e., our result holds for any key registration and secure channel protocol securely realizing ${\cal F}_{{\rm REG}}^{\cal N}$, and ${\cal F}_{{\rm SCS}}$, respectively. The network functionality ${\cal F}_{{\rm NET}^{q}}$ abstract partially global attacker and is a global functionality.

Note that we could not prove 1 W-AKE security for the TAP protocol currently used in Tor as it uses a CCA-insecure version of the RSA encryption scheme.

VI.   Instantiating Secure OR Modules

We present a concrete instantiation of OR modules and show that this instantiation constitutes a set of secure OR modules. As onion algorithms we use the algorithms that are used in Tor with a strengthened integrity mechanism, and as 1 W-AKE we use the recently proposed ntor protocol ^[14].

We prove that the onion algorithms of Tor constitute secure onion algorithms, as defined in Definition 6. The crucial part in that proof is to show that these onion algorithms are predictably malleable, i.e., for every modification of the ciphertext the changes in the resulting plaintext are predictable by merely comparing the modified ciphertext with the original ciphertext. We first show that the underlying encryption scheme, the deterministic counter-mode, is predictably malleable (Section VI-A). Thereafter, we show the security of Tor's onion algorithms (Section VI-B).

In Section VI-C, we briefly present the ntor protocol and cite the result from Goldberg, Stebila, and Ustaoglu that ntor constitutes a 1 W-AKE. The proofs of the lemmas in this section are postponed to the full version ^[1].

A. Deterministic Counter Mode and Predictable Malleability

We show that the deterministic counter-mode (detCTR) scheme is predictably malleable. as defined in Definition 1.

Lemma 1:

If pseudorandom permutations exist, the deterministic counter mode (detCTR) with ${\cal E}_{c}=({\rm G}_{c}, {\rm E}_{c}, {\rm D}_{c}$ as defined in Figure 11 predictably malleable.

Figure 11.Figure 11.

Figure 12.Figure 12.

Figure 13.Figure 13.

B. Security of Tor's Onion Algorithms

Let $pj :=(Gen_{e}, {\it Pinc}, Dec)$ be a stateful deterministic encryption scheme, and let $M :=(Gen_{m}, Mac, V)$ be a deterministic MAC. Let $PRG$ be a pseudo random generator such that for all $x\in\{0,1\}^{\ast}\vert PRG(x)\vert =2\cdot\vert x\vert$. We write $FRG(x)_{1}$ for the first half of $PRG(x)$ and $PRG(x)_{2}$ the second half. Moreover, for a randomized algorithm $A$, we write $A(x;r)$ for a call of $A(x)$ with the randomness $r$.

As a PRP candidate we use AES, as in Tor, and as a MAC use H-MAC with SHA-256. We use that in detCTR encrypting two blocks separately results in the same ciphertext as encrypting the pair of the blocks at once. Moreover, we assume that the output of H-MAC is exactly one block.

The correctness follows by construction. The synchronicity follows, because a PRP is used for the state. The endto-end integrity directly follows from the SUF of the Mac. And the predictable malleability follows from the predictable malleability of the deterministic counter-mode.

C. ntor: a 1W-AKE

Øverlier and Syverson ^[24] proposed a l W-AKE for use in the next generation of the Tor protocol with improved efficiency. Goldberg, Stebila, and Ustaoglu found an authentication flaw in this proposed protocol, fixed it, and proved the security of the fixed protocol ^[14]. We use this fixed protocol, called ntor, as a 1 W-AKE.

The protocol ntor ^[14] is a 1 W-AKE protocol between two parties $P$ (client) and $Q$ (server), where client $P$ authenticates server $Q$. Let $(pk_{Q},sk_{Q})$ be the static key pair for $Q$. We assume that $P$ holds $Q$'s certificate $(Q, pk_{Q)}$. $P$ initiates an ntor session by calling the Initiate function and sending the output message $m_{P}$ to $Q$. Upon receiving a message $m_{P}^{\prime}$, server $Q$ calls the Respond function and sends the output message $m_{Q}$ to $P$. Party $P$ then calls the ComputeKey function with parameters from the received message $m_{Q}^{\prime}$, and completes the ntor protocol. We assume a unique mapping between the session ids $\Psi_{P}$ of the $cid$ in $\Pi_{{\rm OR}}$.

VII.   Forward Secrecy and Anonymity Analyses

In this section, we show that our abstraction ${\cal F}_{{\rm OR}}$ allows for applying previous work on the anonymity analysis of onion routing to $\Pi_{{\rm OR}}$. Moreover, we illustrate that ${\cal F}_{{\rm OR}}$ enables a rigorous analysis of forward secrecy of II_OR

In Section VII-A, we show that the analysis of Feigenbaum, Johnson, and Syverson ^[12] of Tor's anonymity properties in a black-box model can be applied to our protocol $\Pi_{{\rm OR}}$. Feigenbaum, Johnson, and Syverson show their anonymity analysis an ideal functionality ${\cal B}_{{\rm OR}}$ (see Figure 4). By proving that the analysis of ${\cal B}_{{\rm OR}}$ applies to ${\cal F}_{{\rm OR}}$, the UC composition theorem and Theorem 1 imply that the analysis applies to II_OR as well.

In Section VII-B, we present the result that immediate forward secrecy for $\Pi_{{\rm OR}}$ holds, by merely by analyzing ${\cal F}_{{\rm OR}}$. The proofs in this section are omitted due to space constraints but can be found in the full version ^[1].

A. OR Anonymity Analysis

Feigenbaum, Johnson and Syverson ^[12] analyzed the anonymity properties of OR networks. In their analysis, the authors abstracted an OR network against attackers that are local, static as a black-box functionality ${\cal B}_{{\rm OR}}$. We reviewed their abstraction ${\cal B}_{{\rm oR}}$ in Section II-E. In this section, we show that the analysis of ${\cal B}_{{\rm OR}}$ is applicable to $\Pi_{{\rm OR}}$ against local, static attackers.

There is a slight mismatch in the user-interface of ${\cal B}_{{\rm OR}}$ and $\Pi_{{\rm OR}}$, The main difference is that $\Pi_{{\rm OR}}$ expects separate commands for creating a circuit and sending a message whereas ${\cal B}_{{\rm OR}}$ only expects a command for sending a message. We construct for every party $P$ a wrapper $U$ for $\Pi_{{\rm OR}}$ that adjusts $\Pi_{{\rm OR}}$'s user-interface. Recall that we consider two versions of ${\cal B}_{{\rm OR}}$ and $U$ simultaneously: one version in which no message is sent and one version in which a message is sent (denoted as [m]).

Instead of $\Pi_{{\rm OR}}$, $U$ only expects one command: $({\rm send},\, S,\, [m])$. We fix the length $\ell$ of the circuit. Upon $({\rm send},\, S,\, [m]$, $U (\Pi)$ draws the path $P_{1}, \ldots, P_{\ell}\displaystyle\mathop{\leftarrow}_{\$}\ N_{{\rm OR}}$ at random, sends a $({\rm cc}, \langle P, P_{1}, \ldots, P_{\ell}\})$ to $\Pi$, waits for the $cid$ from $\Pi$, and sends a $({\rm send},\, cid,\, m$ command, where $m$ is a dummy message if no message is specified. Moreover, in contrast to ${\cal B}_{{\rm OR}}$ the protocol $\Pi_{{\rm OR}}$ allows a response for a message $m$ and therefore additionally sends a session id $sid$ to a server.^[12]

In addition to the differences in the user-interface, ${\cal B}_{{\rm OR}}$ assumes the weaker threat model of a local, static attacker whereas $\Pi_{{\rm OR}}$ assumes a partially global attacker. We formalize a local attacker by considering $\Pi_{{\rm OR}}$ in the ${\cal F}_{{\rm NET}^{0}}\hbox{-}$ hybrid model, and connect the input/output interface of ${\cal F}_{{\rm NET}^{0}}$ to the wrapper $U$ as well. For considering a static attacker, we make the standard U C-assumption that every party only accepts compromise requests at the beginning of the protocol. Moreover, we also need to assume that ${\cal B}_{{\rm OR}}$ is defined for a fixed set of onion routers ${\cal N}$ in the same way as ${\cal F}_{\rm OR}^{\cal N}$

Finally, our work culminates in the connection of previous work on black-box anonymity analyses of onion routing with our cryptographic model of onion routing.

B. Forward Secrecy

Forward secrecy ^[7] in cryptographic constructions ensures that a session key derived from a set of long-term public and private keys will not be compromised once the session is over, even when one of the (long-term) private keys is compromised in the future. Forward secrecy in onion routing typically refers to the privacy of a user's circuit against an attacker that marches down the circuit compromising the nodes until he reaches the end and breaks the user's anonymity.

It is commonly believed that for achieving forward secrecy in OR protocols it is sufficient to securely erase the local circuit information once a circuit is closed, and to use a key exchange that provides forward secrecy. $\Pi_{{\rm OR}}$ uses such a mechanism for ensuring forward secrecy. Forward secrecy for OR, however, has never been proven, and not even rigorously defined.

In this section, we present a game-based definition for OR forward secrecy (Definition 10) and show that $\Pi_{{\rm OR}}$ satisfies our forward secrecy definition (Lemma 7). We require that a local attacker does not even learn anything about a closed circuit if he compromises all system nodes. The absence of knowledge about a circuit is formalized in the notion of $OR$circuit secrecy (Definition 10), a notion that might be of independent interest.

Recall that we formalize a local attacker by considering $\Pi_{{\rm OR}}$ in the ${\cal F}_{{\rm NET}^{0}}$-hybrid model, i.e., the attacker cannot observe the link between any pair of nodes without compromising any of the two nodes.

Figure 15.Figure 15.

VIII.   Future Work

For future work an interesting direction could be to incorporate hidden services into the UC security analysis. We already designed the abstraction in a way that allows for a modular extension of the UC proof to a hidden service functionality. Moreover, our work offers a framework for the analysis of other desirable OR properties, such as circuit position secrecy.

It is well known that the UC framework lacks a notion of time; consequently any UC security analysis neglects timing attacks, in particular traffic analysis. A composable security analysis that also covers, e.g., traffic analysis, is an interesting task for future work.