Abstract
I. Introduction
Blockchain technologies are emerging as a revolutionary paradigm to perform secure decentralized financial applications. Nevertheless, a widespread adoption of cryptocurrencies, such as Bitcoin [1] and Ethereum [2], is severely hindered by their inherent limitations on transaction throughput [3],[4]. For instance, while Bitcoin can support tens of transactions per second and the confirmation time is about an hour, traditional credit networks like Visa can comfortably handle up to 47,000 transactions per second.
Off-chain protocols [5] are recognized as one of the most promising scalability solutions, achieving a seemingly contradictory property: the bulk of transactions is performed off-chain, and yet in a secure fashion. The idea is to leverage the blockchain only in case of disputes, resorting otherwise to off-chain, peer-to-peer transactions. Bitcoin's Lightning Network [6] is the most widely adopted off-chain instantiation, hosting at the time of writing bitcoins worth more than 170M USD, in a total of more than 27,000 nodes and more than 76,000 channels. In a nutshell, parties deposit money in a shared address, called channel, and can later on perform arbitrarily many off-chain transactions with each other by redistributing the deposit on the channel. In the end, the channel can be closed and the latest state (i.e., deposit distribution) is posted on-chain. Off-chain transactions are not limited to the end-point of the channel, but they can be routed over paths of channels (so-called multi-hop payments). Besides such payment channel networks, an entire ecosystem of off-chain protocols [5] (virtual channels, watchtowers, payment-channel hubs, state channels, side-chains, etc.) is under development for Bitcoin [7]–[12], Ethereum [13]–[16], as well as other cryptocurrencies [17].
The cryptographic protocols underlying these off-chain constructions are rather sophisticated and, most importantly, rely on game-theoretic arguments to discourage malicious behavior. For instance, the Lightning Network relies on a punishment mechanism to disincentivize parties to publish old states on-chain and on an unlocking mechanism where parties first pay a neighbor and then retrieve the paid amount from the other to ensure the atomicity of multi-hop payments (i.e., either all channels are consistently updated or none is).
Off-chain protocols are typically subject to rigorous security analyses, which however concentrate on cryptographic properties and do not capture the game-theoretic ones. In particular, most protocols are proven secure in the Universal Composability framework [18], proving that the cryptographic realization simulates the ideal functionality. This framework, however, was developed to reason about security in the classical honest/Byzantine setting: in particular, the ideal functionality has to model all possible parties' behavior, rational and irrational, otherwise it would not be simulatable, but reasoning on whether or not certain behavior is rational is outside of the model and thus left to informal arguments. This is not just a theoretical issue, but a practical one, as there is the risk to let attacks pass undetected: for instance, the Wormhole attack [7] constitutes a rational behavior in the Lightning Network, which is thus admitted in any faithful model thereof although it undermines its incentive mechanism. The first step towards closing this gap in cryptographic proofs is to come up with a faithful game-theoretic model for off-chain protocols in order to reason about security in the presence of rational parties. We address this challenge in this paper, advocating the use of Extensive Form Games (EFGs) for the game-theoretic security analysis of off-chain protocols. In particular, we introduce two instances of EFGs to model the closing and the routing of the Lightning Network.
A. Related Work
A game-theoretic model for off-chain protocols is initiated and introduced in [19]. This work suffers, however, from several limitations, which make it unsuitable to conduct faithful security analyses. Firstly, the game model considers only honest closing of channels, i.e., all deviations - such as posting an old state - are ignored: this makes it impossible to reason about the security of basic channel operations. Secondly, the pay-offs are represented as constants, which neglects the dependency of the channel's balance on its security properties. Further, fees are not considered at all, thereby ignoring their impact on Lightning protocols. For instance, the routing game to model the security of multi-hop payments fails to capture already identified attacks in payment channel networks, like the Wormhole attack [7] that targets the fee distribution among players. Additionally, Lightning is vulnerable to the Griefing attack [20], where a significant amount of money is locked. In our work, we overcome the aforementioned limitations, by defining a stronger closing phase model, by aligning the utilities to the monetary outcome, by considering all possible deviations of parties during closing, and by revising the relevant security properties. We demonstrate the importance of precision in game-theoretic protocol models by modeling the Wormhole attack, as well as the Griefing attack.
Our work further complements other game-theoretic advancements in the area, most prominently the following lines of research.
- Incentivizing Watchtowers: A major drawback of payment channel protocols is that channel participants must frequently be online and watch the blockchain to prevent cheating. To alleviate this issue, the parties can employ third parties, or so-called watchtowers, to act on their behalf in case their counterparty misbehaves. Correctly aligning the incentives of watchtowers to yield a secure payment channel protocol is, however, challenging. This is the main focus of several works [11],[15],[16],[21]. As their objective is to incentivize external parties, their models does not apply in our work.
- Payment Channel Network Creation Games: Avarikioti et al. [22],[23] study payment channel networks as network creation games. Their goal is to determine which channels a rational node should establish to maximize its profit. Ersoy et al. [24] undertake a similar task; they formulate the same problem as an optimization problem, show it is NP-hard, and present a greedy algorithm to approximate it. Similarly to our work, all these works assume rational participants. However, we aim to model the security of the protocols, in contrast to these works that study the network creation problem graph-theoretically.
- Blockchains with Rational Players: Blockchains incentivize miners to participate in the network via monetary rewards [1]. Therefore, analyzing blockchains under the lens of rational participants is critical for the security of the consensus layer. There are multiple works in this direction: Badertscher et al. [25] present a rational analysis of the Bitcoin protocol. Eyal and Garay [26] introduce an attack on the Nakamoto consensus, effectively demonstrating that rational miners will not faithfully follow the Bitcoin protocol. This attack is generalized in [27],[28]. Consequently, Kiayias et al. [29] analyze how miners can deviate from the protocol to optimize their expected outcome. Later, Chen et al. [30] investigate the reward allocation schemes in longest-chain protocols and identify Bitcoin's allocation rule as the only one that satisfies a specific set of desired properties. On a different note, several works study the dynamics of mining pools from a game-theoretic perspective [31],[32] or introduce network attacks that may increase the profit of rational miners [33],[34]. An overview of game-theoretic works on blockchain protocols can be found in [35].
All these works, however, focus on the consensus layer (Layer-1) of blockchains and as both the goals and assumptions are different from the application layer (Layer-2), the models introduced there cannot be employed for our purposes. For instance, payment channel protocols occur off-chain and thus game-based cryptographic assumptions of the blockchain do not apply. In addition, consensus protocols investigate the expected reward of miners which is a probabilistic problem, whereas we ask if any honest player could lose money, which depends on the behavior of the other players and is fundamentally deterministic.
Game-based definitions have also been proposed for the security analysis of smart contracts [36],[37]. These models, however, target an on-chain setting and are thus not suitable to reason about the specifics of off-chain constructions (e.g., closing games, routing games, etc.).
B. Our Contributions
In this work, we take the first steps towards closing the gap between security and game-theoretic analysis of off-chain protocols. Specifically, we introduce the first game-theoretic models that are expressive enough to reason about the security of off-chain protocols. We model off-chain protocols as games and then analyze whether or not certain security properties are satisfied. The design of our models is driven by two principles: (a) all possible actions should be represented and (b) the utility function should mirror the monetary outcome realistically. We aim to ensure that honest participants do not suffer any damage (P1), whereas deviating from the protocol yields a worse outcome for the adversary (P2) We will use weak immunity (Definition II.4) to implement (P1), and collusion resilience (Definition III.8) together with practicality (Definition III.7) for (P2). While we believe that our approach of implementing principles (a) and (b) is easily extensible to other off-chain protocols, in this work we focus on the Bitcoin Lightning Network, which constitutes the most widely adopted off-chain protocol. Our technical contributions can be summarized as follows:
- We refine existing game-theoretical concepts in order to reason about the security of off-chain protocols (Section III).
- We introduce the Closing Game G_{c}, the first game-theoretic security model that accurately captures the closing phase of Lightning channels, encapsulating arbitrary deviations from the protocol specification (Section IV).
- We perform a detailed security analysis of G_{c}, formalize folklore security corner cases of Lightning, and present the strategy that rational parties should follow to close their channels in order to maximize their expected out-come relative to the current and previous distribution states (Section V).
- We identify limitations in prior work [19] on game-based modeling of multi-hop payments, putting forward a new game-based definition that is precise enough to cover the Wormhole and the Griefing attack (Section VI). We further show how to model Fulgor protocol [38], a variant of Lightning's routing that prevents the Wormhole attack. Our formalization leverages game theory concepts introduced in Section III and Section IV, thereby demonstrating the theoretical expressiveness of our framework to analyze complex protocols..
In conclusion, our work brings game-theoretical foundations to enforce security of off-chain protocols, by providing a rigorous analysis over security properties expressed through formal requirements over game strategies. We believe, the provided rigor in our paper opens up new venues for automating security analysis via game-theoretic arguments, a challenge which we aim to tackle in future work.1
II. Background and Preliminaries
A. Payment Channel Networks
A payment channel [8] can be seen as an escrow (or multi-signature), into which two parties Alice A and Bob B transfer their initial coins with the guarantee that their coins are not locked forever and the agreed balance can be withdrawn at any time. After that, A and B can pay each other off-chain by signing and exchanging messages that reflect the updated balances in the escrow. These signatures can be used at any time to close the channel and distribute the coins on-chain according to the last channel state. In order to discourage parties from posting an old state on-chain, a punishment mechanism is in place. In particular, in Lightning [6], once A closes the channel, she has to wait a mutually agreed time before getting her coins. Meanwhile, B has the opportunity to withdraw all the coins in the channel (by posting a so-called revocation transaction), including the ones assigned to A, if the state posted on-chain by A is not the last one they mutually agreed on. Such a punishment mechanism is of game-theoretic nature: parties can indeed post an old state on-chain, yet they are discouraged to do so.
In particular, Lightning payment channels operate as follows: First, Alice and Bob create a funding transaction where they input their respective coins; the funding transaction has a single output that can only be spent if both A and B provide their signature (2-out-of-2 multi-signature). Then, the two parties create the first commitment transaction, i.e., a transaction that spends the output of the funding transaction and returns the initial coins to both parties. In other words, the input of the commitment transaction is the output of the funding transaction while the output of the first commitment transaction is two-fold: the first output returns the coins to A and the second output to B. However, the commitment transaction each party holds is not the same. Specifically, the commitment transaction of A has an additional spending condition, a timelock t that signifies the revocation period and is pre-agreed between the two parties; in A's commitment transaction B's output is spendable immediately. Symmetrically, in B's commitment transaction B's output has a timelock t while A's output is spendable immediately. Note that a timelock t is a condition that allows the coins of the output to be spent on-chain only after time t has elapsed from the publication of the transaction. After A and B sign and exchange the respective first commitment transactions, they proceed to signing the funding transaction and publishing it on-chain. This order is important to avoid hostage situations2. As soon as the funding transaction is securely published on-chain, A and B can transact off-chain by creating every time a new commitment transaction that depicts the current balance of the joint capital among the two parties. Every time a new commitment transaction is created, the parties reveal a secret to their counterparty that allows their counterparty to spend their own coins immediately (e.g., A can spend B's coins from the previous commitment) if the previous commitment transaction appears on chain (revocation transaction). To close a Lightning channel, the two parties can either collaborate and spend the output of the funding transaction, or each of them can close the channel unilaterally by publishing the last commitment transaction. Since the commitment transactions each party hold have a timelock, in case of cheating, i.e., publication of a previous commitment transaction on-chain, the counterpart can immediately spend the cheating party's coins, claiming all the coins of the channel, thus punish the cheating party for misbehaving.
Technically, A and B do not just lock their initial funds but also a certain small amount which will be used as a fee for the closing transaction of the channel. Note that every on-chain transaction requires such a fee f. The fee for the opening transaction is paid upon the opening of the channel and is thus irrelevant to our consideration. However, in case A posts an old state on-chain and B performs the revocation transaction - which is an on-chain transaction - to prove it, B has to carry the additional transaction fee alone. These facts have an important impact on our game-theoretic models.
In the following, we refer to honest closing when a party unilaterally closes the channel by posting the last commitment transaction or when the parties close collaboratively, where both parties sign to spend the funding transaction output directly.
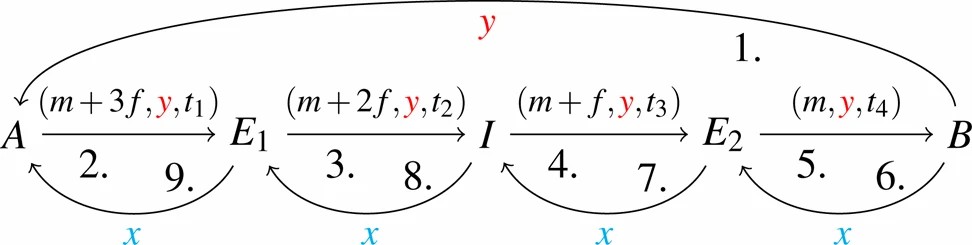
Fig. 1.Fig. 1. Routing in lightning using htlcs.
Off-chain transactions are not limited to the end-points of a channel, as they can be performed whenever sender and receiver are connected by a path of channels with enough capacity. The cryptographic approach to do so exploits hash-time-locked-contracts (HTLC) [12]. Assume players A and B do not share a channel. Instead, A has a channel with E_{1};\ E_{1} has a channel with I;\ I has a channel with E_{2}; and E_{2} has a channel with B, as illustrated in Figure 1. Player A can now send an amount m to player B via the intermediaries E_{1},I and E_{2}, where each intermediary charges a fee f for the routing service, hence A should pay m+3f. The core idea is that A pays E_{1},\ E_{1} pays I, and so forth, until B gets paid.
A key security property in multi-hop payments is atomicity: either all payments are successful, and the deposit in each channel is updated accordingly, or none is. To achieve this property, the Lighting protocol proceeds as follows. First, the receiver B generates a secret x and sends its hash h(x)=y to the sender A (see action 1 in Figure 1). Then A creates an HTLC for E_{1}, where she locks m+3f with lock y and time-out t_{1}. That means only E_{1} can claim the money and only by providing a value whose hash is y within time t_{1} (action 2 in Figure 1). Although E_{1} does not know such a value yet and can therefore not unlock, E_{1} can nevertheless proceed by creating another HTLC for I also locked with y and a time-out t_{2} (action 3 in Figure 1). Thereafter, I and E_{2} continue in the same way (actions 4 - 5 in Figure 1). Actions 1 - 5 of Figure 1 are called the locking phase . Note that in order to allow everybody to unlock their HTLCs in the subsequent steps, the time-outs have to be decreasing t_{1} > t_{2} > t_{3} > t_{4}. Once B receives the conditional payment, he can reveal x to E_{2} and the conditional payment is unlocked (action 6 in Figure 1). The others can now unlock the HTLCs one after the other from right to left (actions 7 - 9 in Figure 1), which is called the unlocking phase . Finally, A paid m+3f,\ B received m and each intermediary was rewarded with f.
We note that atomicity is achieved by a game-theoretic argument: intermediaries can, in principle, stop the protocol either in the locking phase or in the unlocking phase. In the former, they would lose the transaction fee f, while in the latter, they would lose the payment amount m, m+f, m+2f respectively. Thus, they are incentivized to act once they have committed to participate.
a) The Wormhole Attack
The aforementioned routing protocol is proven to be vulnerable to the Wormhole attack [7], which is depicted in Figure 2. The attack is as follows: E_{1} and E_{2} collude, and bypass I in the unlocking phase, thus stealing I^{\prime}\mathrm{s} participation reward f. Until actions 6 in Figure 1 and Figure 2, the behavior is identical. Then, E_{2}, knowing x, forwards x to E_{1} (offline) instead of unlocking the HTLC from I (action 7 in Figure 2). This way, E_{1} can unlock A^{\prime}\mathrm{s} HTLC and claim the money (action 8), but I will never be able to unlock. After a certain time the remaining HTLCs time-out and
the locked money returns to the creators.
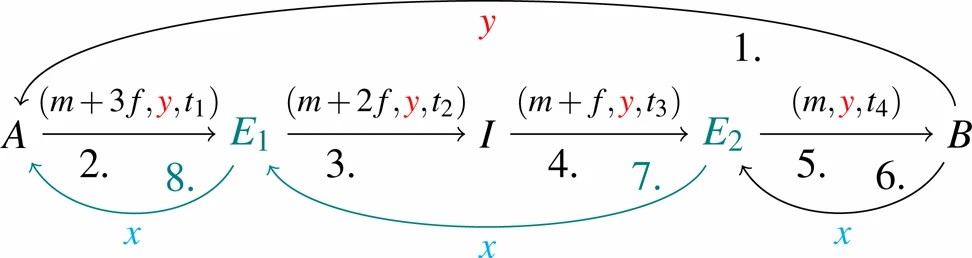
Fig. 2.Fig. 2. Wormhole attack in lightning.
Therefore, the parties A and B are not affected. However, E_{1} and E_{2} collectively earn 3f instead of the 2f they deserve, stealing the fee f from I, who locked resources in the locking phase of the protocol. This attack undermines the incentive of intermediaries to route payments.
b) The Griefing Attack
It describes the scenario when a player, assume B for simplicity, ignores the proposed payment and refuses to proceed [20]. This way, money is locked in the conditional payments for a considerable amount of time. While [40] studies the Griefing attack through probabilistic modelling and [41] provides mitigation techniques, to the best of our knowledge there is no formal security analysis of this attack at present. Our work addresses this limitation and shows that Lightning's routing module is indeed susceptible to the Griefing attack.
In the sequel we consider the behavior as illustrated in Figure 1 as the only honest routing behavior.
B. Game-Theoretic Definitions
We now introduce the game-theoretic concepts relevant for our formalization. We denote real numbers by \mathbb{R} and tuples as \sigma=(\sigma_{1},\ldots,\sigma_{n}). We write \sigma[\sigma_{i}^{\prime}/\sigma_{i}] to denote the tuple resulting from substituting \sigma_{i} by \sigma_{i}^{\prime} in \sigma, that is \sigma[\sigma_{i}^{\prime}/\sigma_{i}]= (\sigma_{1},\ldots,\sigma_{i-1},\sigma_{i}^{\prime},\sigma_{i+1},\ldots,\sigma_{n}). We understand games as static objects in which finitely many players can choose finitely many times from a finite set of actions. A game yields a certain positive or negative utility for each player. We briefly overview the very common Normal Form Games, also called Strategic Games [42], in which each player chooses an action only once , called strategy.
Definition II.1 (Normal Form Game - NFG)
A Normal Form Game (NFG) is a tuple \Gamma=(N,\mathscr{S},u), where Nis the set of game players, \mathscr{S}=\times_{p\in N}\mathscr{S}_{p}the set of joint strategies \sigma and uthe utility function:
- \mathscr{S}_{p}is the non-empty set of strategies player pcan choose from. Thus, a joint strategy \sigma\in\mathscr{S}is a tuple of strategies \sigma=(\sigma_{p_{1}},\ldots,\sigma_{p_{\vert N\vert }})with \sigma_{p_{j}}\in \mathscr{S}_{p_{i}}.
- u=(u_{p_{1}},\ldots,u_{p_{n}}), where u_{p_{i}}:\mathscr{S}\rightarrow \mathbb{R}assigns player p_{i}its utility for every joint strategy \sigma\in\mathscr{S}.
In what follows we fix an arbitrary game \Gamma and give all definitions relative to it. To formalize an optimal outcome on game strategies, we use Nash Equilibria.
Definition II.2 (Nash Equilibrium - NE)
A Nash Equilibrium is a joint strategy \sigma\in \mathscr{S}\ s.t, no player p_{i}can increase their utility by unilaterally deviating from \sigma=(\sigma_{p_{1}},\ldots,\sigma_{p_{\vert N\vert }}), Formally , \begin{equation*}\forall p\in N\ \forall\sigma_{p}^{\prime}\in \mathscr{S}_{p}:u_{p}(\sigma)\geq u_{p}(\sigma[\sigma_{p}^{\prime}/\sigma_{p}]). \tag{1}\end{equation*}
Another important concept is weakly dominated strategies , expressing the strategies a rational player would not play since they yield worse utilities.
Definition II.3 (Weakly Dominated Strategy)
A strategy \sigma_{p}^{d}\in \mathscr{S}_{p}of player pis called weakly dominated by strategy \sigma_{p}^{\prime}\in \mathscr{S}_{p}, if it always yields a utility at most as good as \sigma_{p}^{\prime}and a strictly worse utility at least once: \begin{align*}&\forall\ \sigma \in\mathscr{S}: u_{p}(\sigma[\sigma_{p}^{d}/ \sigma_{p}])\leq u_{p}(\sigma[\sigma_{p}^{\prime}/ \sigma_{p}])\ and \tag{2}\\ &\exists\ \sigma \in \mathscr{S}: u_{p}(\sigma[\sigma_{p}^{d}/ \sigma_{p}]) < u_{p}(\sigma[\sigma_{p}^{\prime}/ \sigma_{p}]). \tag{3}\end{align*}
Example II.1
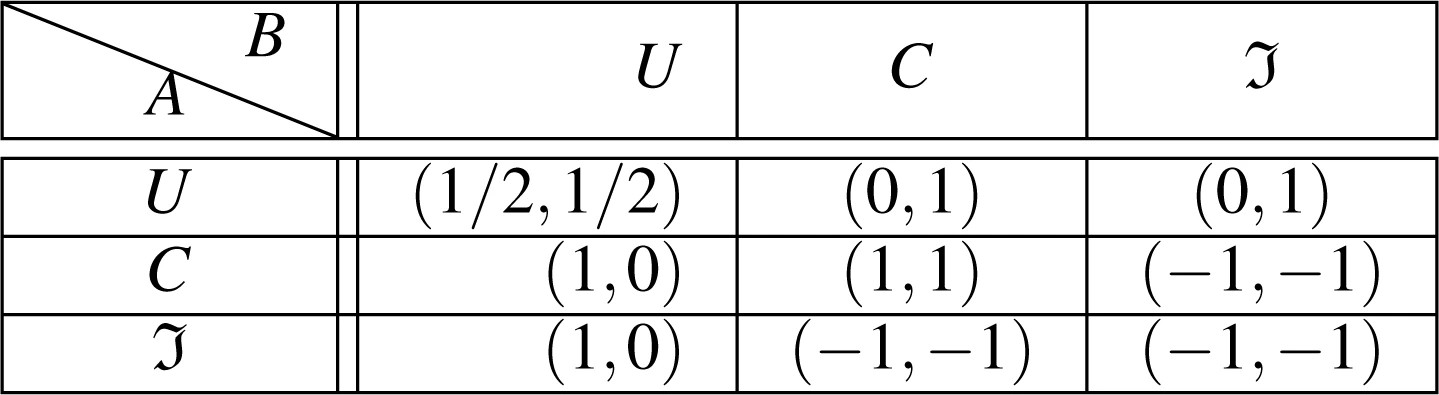
Consider the NFG\ \Gamma_{C} in Table I,which was introduced in [19] to model closing. In this game \Gamma_{C}, there are two players N=\{A,B\}and each players can choose from the same strategy set \mathscr{S}_{A}=\mathscr{S}_{B}=\{U,C,\Im\}. Here, strategy Ucaptures unilateral closing, that is publishing the latest state on-chain. Further, strategy Ccorresponds for closing collaboratively, that is publishing a mutually signed transaction. Finally, strategy \Imstands for ignoring, that is doing nothing. The utility for each joint strategy is given in Table I, where player A^{\prime}sstrategies are listed in the left column of Table I, and the strategies of Bare given in the top row of Table I .
Applying Definition II.2, the joint strategies (C,C),\ (U,\Im) and (\Im, U)are Nash Equilibria: for each of these joint strategies, neither Anor Bcan deviate in order to increase their own utility. Comparing the second and the third row of Table I, we see that A's utility is always as least as good in the second row as it is in the third row. Hence, strategy Cweakly dominates strategy \Imfor player A, by Definition II.3; the same property also holds for player B. By comparing the other pairs of rows/columns of Table I, we see that there is no other weak dominance in \Gamma_{C}.
C. Game-Theoretic Security Properties of Off-Chain Protocols
We now present existing game-theoretic concepts [19],[42] implying security properties of off-chain protocols. In Section III, we extend these concepts towards another type of games, called Extensive Form Games, enabling our security analysis in Section IV. We focus on two security properties ensuring that (P1) honest players do not suffer damage, and (P2) subgroups of rational players do not deviate from a respective strategy. A protocol is compliant to these properties, if the strategy implementing the intended behavior satisfies them; we call such a strategy an honest strategy .
(P1) No Honest Loss . As the utility function of a game is supposed to display the monetary and intrinsic value of a certain joint strategy, property (P1) is expressed using weak immune strategies defined next.
Definition II.4 (Weak Immunity)
A joint strategy \sigma\in\mathscr{S} in an NFG\ \ \Gammais called weak immune, if every player pthat follows \sigmagets utility at least 0, regardless of how the other players behave: \begin{equation*}\forall p\in N\ \forall\sigma^{\prime}\in \mathscr{S}: \quad u_{p}(\sigma^{\prime}[\sigma_{p}/\sigma_{p}^{\prime}])\geq 0. \tag{4}\end{equation*}
Example II.2
In the game \Gamma_{C}of Table I, the only weakly immune strategy is (U, U). This is the case, because as long as A chooses U, player Bcan take any strategy and Awill never get negative utility (similarly, vice-versa) .
(P2) No Deviation . Even though the concept of Nash Equilibria seems to be a good candidate to ensure (P2) at first glance, they have two crucial shortcomings. First, a Nash Equilibrium only ensures that a single player cannot profit from deviating, but does not imply that two or more players cannot do so. Second, there might be Nash Equilibria, which are weakly dominated by another strategy for a specific player. Such Nash Equilibria will therefore not be played by rational parties and hence should not be considered to satisfy (P2).
The solution proposed for NFGs in [19] is to consider strategies \sigma compliant to (P2), if they are both strongly resilient (fixing the former shortcoming) and practical (fixing the latter) as defined subsequently.
Strong resilience extends Nash Equilibria by considering deviations of multiple players.
Definition II.5 (Strong Resilience - SR)
A joint strategy \sigma\in\mathscr{S}in an NFG\ \Gamma is strongly resilient (SR) if no proper subgroup of players S:=\{s_{1},\ldots,s_{j}\}has an incentive in deviating: \begin{align*}\forall S\subset N\ \ & \forall \sigma_{s_{i}}^{\prime}\in \mathscr{S}_{s_{i}}\quad \forall p\in S:\\& u_{p}(\sigma)\geq u_{p}(\sigma[\sigma_{s_{1}}^{\prime}/ \sigma_{s_{1}}, \ldots, \sigma_{s_{j}}^{\prime}/ \sigma_{s_{j}}]). \tag{5}\end{align*}
We note that in games with two players (i.e. two-player games), strong resilience and Nash Equilibrium are identical. As such, in \Gamma_{C} from Table I, the joint strategies (C,C),\ (U,\Im) and (\Im, U) of Example II.1 are also strongly resilient.
To define practicality of a strategy, we first introduce the concept of iterated deletion of weakly dominated strategies (IDWDS) .
Definition II.6 (Iterated Deletion of Weakly Dominated Strategies - IDWDS)
The iterated deletion of weakly dominated s trategies (IDWDS) of an NFG\ \Gammais defined as iteratively rewriting \Gammaby omitting all weakly dominated strategies of all players. This is repeated until no strategy is weakly dominated any more. The resulting game \Gamma^{\prime}is thus a subgame of \Gamma.

Note that, when IDWDS is applied to a game \Gamma, then every Nash Equilibrium of the resulting game \Gamma^{\prime} is also a Nash Equilibrium of \Gamma. Since all weakly dominated strategies of every player are removed at each step, the generated game is unique. Details and proofs can be found in [42].
We now define practical strategies, in order to ensure that no single strategy is weakly dominated at any iteration.
Definition II.7 (Practicality)
A strategy is practical if it is a Nash Equilibrium of the NFG\ \Gamma^{\prime}after iterated deletion of weakly dominated strategies .
Example II.3
Let us consider \Gamma_{C}from Table I. We know from Example II.1 that only \Imis weakly dominated for both Aand B. Therefore, according to Definition II.6 strategy \Imhas to be removed from both player's strategy set. This yields the game \Gamma_{C}^{\prime}as listed Table II .
Note that there are no weakly dominated strategies in \Gamma_{C}^{\prime}. Thus, any Nash Equilibrium of \Gamma_{C}^{\prime}is also practical strategy of \Gamma_{C}. By comparing utilities, we derive that the only Nash Equilibrium of \Gamma_{C}^{\prime}is the joint strategy (C,C).
An alternative approach for expressing (P2) is by requiring a strategy \sigma to be both a strong Nash Equilibrium (a property similar to SR ) and practical, instead of SR and practical.
Definition II.8 (Strong Nash Equilibrium - sNE)
A joint strategy \sigma is a strong Nash Equilibrium (sNE) if for every group of deviating players S:=\{s_{1},\ldots,s_{j}\}and all possible deviations \sigma_{s_{i}}^{\prime}\in \mathscr{S}_{s_{i}},\ i\in\{1,\ldots,j\}at least one player p\in Shas no incentive to participate, that is \begin{align*}\forall S \subseteq N, S \neq \emptyset \quad & \forall \sigma_{s_{i}}^{\prime} \in \mathscr{S}_{s_{i}} \quad \exists p \in S:\\& u_{p}(\sigma) \geq u_{p}(\sigma[\sigma_{s_{1}}^{\prime} / \sigma_{s_{1}}, \ldots, \sigma_{s_{j}}^{\prime} / \sigma_{s_{j}}]).\tag{6}\end{align*}
Example II.4
In \Gamma_{C}from Table I, all NE are also sNE. For the joint strategy (C,C), this is easy to see. However, it is also the case for (U,\Im) and (\Im, U), since any deviation yields a utility of at most 1. Thus, at least one player's utility does not increase by deviating from (U,\Im), (\Im,U)respectively .
A detailed comparison of the various concepts ensuring (P2) including their strengths and weaknesses, is given in Section III.
III. Efg-Based Modeling of Off-Chain Protocols
So far we considered games in which each party takes only one action. We now extend our definitions to handle adaptive strategies, i.e., games in which parties take several actions and choose at each step which action to take based on the actions previously chosen by other parties. As we will see, this is necessary for faithfully modeling off-chain protocols and overcoming the limitations of previous work [19]. For that, we overview the concept of extensive form games (EFGs) in Section III-A. We show how to lift NFG-based security definitions to EFGs in Section III-B. Finally, we show that these definitions do not yet suffice to yield an accurate security model of off-chain protocols, and introduce a refined security definition based on the concept of collusion resilience in Section III-C.
A. Extensive Form Games (efg)
To formalize strategies where players make multiple choices one after the other, we advocate the usage of Extensive Form Games (EFGs) [42], which extend NFGs as follows.
Definition III.1 (Extensive Form Game - EFG)
An Extensive Form Game (EFG) is a tuple \Gamma=(N,\mathscr{H},P,u), where N and uare as in NFGs. The set \mathscr{H}captures game histories, \mathscr{T}\subseteq \mathscr{H}is the set of terminal histories, and Pdenotes the next player function, satisfying the following properties .
• The set \mathscr{H}of histories is a set of sequences of actions with
- \emptyset\in \mathscr{H};
- if the action sequence (a_{k})_{k=1}^{K}\in \mathscr{H} and L < K, then also (a_{k})_{k=1}^{L}\in \mathscr{H};
- a history is terminal (a_{k})_{k=1}^{K}\in\mathscr{T}, if there is no action a_{K+1}with (a_{k})_{k=1}^{K+1}\in \mathscr{H}.
• The next player function P
- assigns the next player p\in Nto every non-terminal history (a_{k})_{k=1}^{K}\in \mathscr{H}\backslash \mathscr{T}, that is P((a_{k})_{k=1}^{K})=p;
- after a non-terminal history h=(a_{k})_{k=1}^{K}\in \mathscr{H}it is player P(h)^{\prime}s\ turnto choose an action from the action set A(h)=\{a:(h,a)\in \mathscr{H}\}.
A strategy of player pis a function \sigma_{p}mapping every h\in \mathscr{H}with P(h)=pto an action from A(h). Formally , \begin{equation*}\sigma_{p}:\{h\in \mathscr{H}:P(h)=p\}\rightarrow\{a:(h,a)\in \mathscr{H},\forall h\in \mathscr{H}\},\end{equation*}such that \sigma_{p}(h)\in A(h). The set of all strategies of a player p is \mathscr{S}_{p}, and the set of all joint strategies is \mathscr{S}=\times _{p\in N}\mathscr{S}_{p}.
Note that the set of terminal histories \mathscr{T} is uniquely determined by \mathscr{H} and therefore does not explicitly occur in the tuple \Gamma. Since histories h are just sequences of actions h=(a_{k})_{k=1}^{K}=(a_{1},\ldots,a_{K}), we denote histories by the variable h, the abstract sequence (a_{k})_{k=1}^{K}, or the explicit sequence (a_{1}, \ldots,a_{K}), depending on the context in which they are used. We note that EFGs can conveniently be represented as trees, as described below.
Definition III.2 (EFG as Tree)
Considering an EFG\ \Gamma= (N,\mathscr{H},P,u), the following tree G=(V,E)represents \Gamma.
- For every history h\in \mathscr{H}, there exists exactly one node v_{h}\in V. This is labeled by P(h), the next player, if his not terminal (h\not\in\mathscr{T}), or by u(\sigma), the joint utility of playing a game with history h, if his terminal (h\in\mathscr{T})and the joint strategy \sigmayields history h.
- Two nodes v_{h},\ v_{h^{\prime}}\in \mathscr{H}are connected via an oriented edge (v_{h},v_{h^{\prime}})\in E\ \ iff\ \ h^{\prime}=(h,a). This edge is labeled a.
Let us illustrate EFGs and their tree-based representation through the following example.
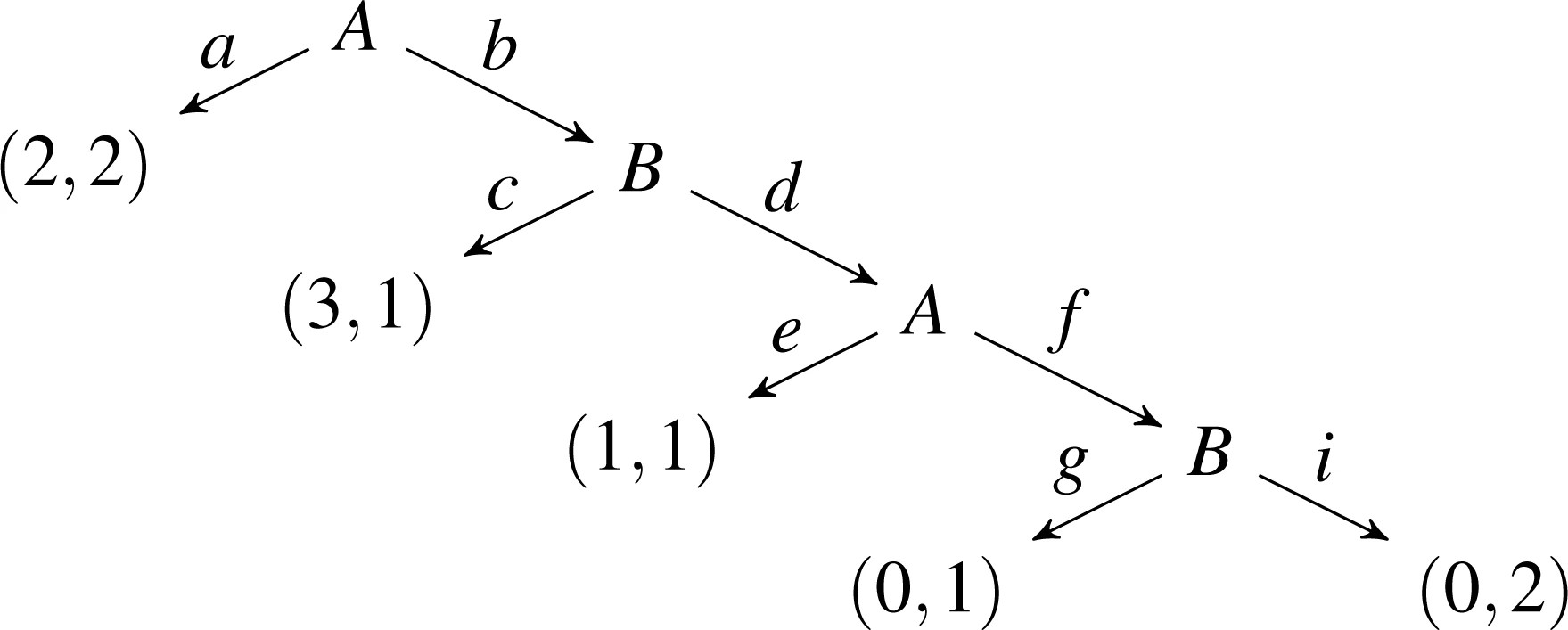
Fig. 3.Fig. 3. An efg \Gamma_{E}.
Example III.1
The game tree in Figure 3 results from the extensive form game \Gamma_{E}=(N,\mathscr{H},P,u)with the two players N=\{A,B\}, where the set of histories is \mathscr{H}=\{\emptyset, (a), (b), (b,c), (b,d), (b,d,e), (b,d,f), (b,d,f,g), (b,d,f,i)\}. The next player function Passigns player Aafter histories \emptyset and (b,d), and player Bafter (b) and (b,d,f). Finally, the utility function uassigns joint utility (2,2) to strategies that yield history (a), utility (3,1) for strategies with history (b,c), utility (1,1) for strategies with history (b,d,e), and (0,2) for strategies resulting in (b,d,f, i). A strategy \sigma=(\sigma_{A}, \sigma_{B}) in \Gamma_{E}is for example: A chooses aafter history \emptyset:\sigma_{A}(\emptyset)=a; and fafter (b,d):\sigma_{A}((b,d))=f;\ Btakes cafter (b):\sigma_{B}((b))=c, and gafter (b,d,f):\sigma_{B}((b,d,f))=g. Following this strategy until we read a leaf yields history (a). A different strategy \sigma^{\prime}=(\sigma_{A}^{\prime}, \sigma_{B}^{\prime}), which also yields history (a), is for example \sigma_{A}^{\prime}(\emptyset)=a,\ \sigma_{A}^{\prime}((b,d))=e and \sigma_{B}^{\prime}=\sigma_{B}.
As depicted in the tree-based representation of Figure 3, we note that the utility of joint strategies in an EFG is uniquely determined by their associated history (i.e., path). In the context of EFGs, the concept of Nash Equilibria remains as given in Definition II.2. In addition to Nash Equilibria, another useful concept for EFGs is the Subgame Perfect Equilibrium , which we will use to characterize the strategies played in practice by rational parties. To this end, we first introduce the notion of subgames of EFGs. A subgame of an EFGs can be seen as a subtree determined by a certain history (i.e., whose root note is the last history node), and is formalized below.
Definition III.3 (Subgame of EFG)
The subgame of an EFG\ \Gamma=(N,\mathscr{H},P, u)associated to history h\in \mathscr{H}is the EFG\ \Gamma(h)=(N, \mathscr{H}_{\vert h},P_{\vert h}, u_{\vert h})defined as follows: \mathscr{H}_{\vert h}:= \{h^{\prime}\ \vert\ (h,h^{\prime})\in \mathscr{H}\},\ P_{\vert h}(h^{\prime}): =P(h,h^{\prime}), and u_{\vert h}(h^{\prime}):=u(h,h^{\prime}).
Example III.2
Consider the EFG\ \Gamma_{E}from Figure 3. The subgame of \Gamma_{E}associated to history (b,d)is the subtree rooted in A.
By adjusting the concept of Nash Equilibrium to subgames, we derive the following property of joint strategies.
Definition III.4 (Subgame Perfect Equilibrium)
A subgame perfect equilibrium is a joint strategy \sigma=(\sigma_{1},\ldots,\sigma_{n})\in \mathscr{S},s.t \sigma_{\vert h}=(\sigma_{1\vert h},\ldots,\sigma_{n\vert h})is a Nash Equilibrium of the subgame \Gamma(h), for every h\in\mathscr{H}. The strategies \sigma_{i\vert h}are functions that map every h^{\prime}\in \mathscr{H}_{\vert h}with P_{\vert h}(h^{\prime})=ito an action from A_{\vert h}(h^{\prime}).
B. Efg Extensions for Security Properties
While EFGs enable us to incorporate choices made at different times yielding different options for the next player, they come with the following limitation. The intended (i.e., honest) behaviors in off-chain protocols only specify a terminal history (i.e., a path from root to leaf), rather than a strategy. For instance, an honest history may specify to close the channel collaboratively, but it does not capture a player's behavior once a player deviated. To address this limitation, we introduce the following notion of an extended strategy in EFGs.
Definition III.5 (Extended Strategy)
Let \betabe a terminal history in an EFG\ \Gamma. Then, all strategies \sigma_{\beta}that result in history \beta are extended strategies of \beta.
Example III.3
Recall Figure 3. In Example III.1. we consider the terminal history (a)and provide two extended strategies of (a), they are \sigma and \sigma^{\prime}. A strategy, which is not an extended strategy of (a)is for instance \sigma^{\prime\prime}=(\sigma_{A}^{\prime\prime}, \sigma_{B}^{\prime\prime}), where \sigma_{A}^{\prime\prime}(\emptyset)= b,\ \sigma_{A}^{\prime\prime}((b,d))=e and \sigma_{B}^{\prime\prime}=\sigma_{B}. This is the case because by following the choices of A and B in \sigma^{\prime\prime}, we end up in (b,c).
While EFGs can in principle be translated to NFGs, as explained in [43], analyzing the security properties (P1)-(P2)over the translated NFGs may yield unexpected results. We shortly exemplify this point in Example III.4, but similar issues occur also in larger games. We thus lift NFG-based definitions to EFGs, enabling the analysis of (P1) and (P2). Since EFGs have a utility function just as NFGs do, which assigns values after the game, the NFG concepts of weak immunity, strong resilience and sNE remain the same for EFGs.
Definition III.6
(EFG Properties). A joint strategy \sigma\in \mathscr{H}of an EFG\ \Gammais called weak immune, strongly resilient, or a strong Nash Equilibrium, if it satisfies the formulae of Definition II.4Definition II.5 or Definition II.8 respectively .
Practicality in NFGs, however, relies on IDWDS, which fails to incorporate the sequential nature of EFGs, and hence must be adjusted for EFGs. This is because NFG actions happen simultaneously, while EFG players choose their actions sequentially. We first present an example to showcase that applying the NFG definition of practicality to an EFG, by using its translation to an NFG, leads to overlooking rational strategies.
Example III.4
Let us consider the EFG\ \Gamma_{E}from Figure 3 with two players Aand B. The compact translation of \Gamma_{E}to an NFG\ \Gamma_{N}is given in Table III. Histories of Figure 3, where players choose twice, such as (b,d,f), are translated to Table III as the joint strategy (b;f,d). Hence, the NFGstrategy b;fof player Ameans choosing action bfirst, and, if A gets to choose again , Atakes f. Player A^{\prime}sstrategies are displayed in the rows, whereas player B^{\prime}sare shown in the columns of Table III. Strategy d;gfor example denotes choosing din the first turn and gin the second turn, unless the game ends before. For readability, strategies with identical utilities in any case are merged together, e.g., having only a instead of both a;e and a;f.
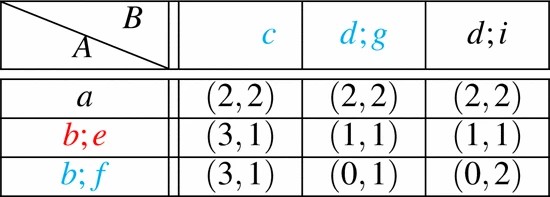
According to definition of practicality for NFGs (see Definition II.7), the only practical strategy in \Gamma_{N} is (a, d;i), which results in a utility of (2,2). This is because for Astrategy b;eweakly dominates b;fand for Bstrategy d;iweakly dominates both c and d;g. After deleting those (in blue), the red strategy b;e\ of\ Abecomes weakly dominated by a. Thus, after removing b;eonly the joint strategy (a,d;i)remains and is therefore a Nash Equilibrium of the resulting game .
However, in the EFG\ \Gamma_{E}the comparison of strategies has a certain order, as not all choices are made simultaneously. Thus, when it comes to Bchoosing between option c and d, choosing cis also a rational action because in any case Bgets utility 1. This is the case, since the subgame following after d, will end in the subgame perfect and practical (1,1), if played by rational players. Following this argumentation, we claim that (b;e,c), yielding history (b,c)should also be considered rational and thus practical .
Example III.4 demonstrates that it is advisable to adapt the NFG concept of practicality for EFGs, and that a näive application can be problematic since information may be lost during the transformation from EFG to NFG [42]. We therefore propose to use subgame perfect equilibria for comparing EFG strategies, and define practicality for EFGs as follows.
Definition III.7 (Practicality for EFG)
A strategy of an EFG \Gamma is practical if it is a subgame perfect equilibrium of \Gamma.
C. Security Strategies for Off-Chain Protocols
We now leverage the previously introduced EFG-based definitions (Section III-B1) to faithfully model the security of off-chain protocols. In particular, we propose the novel concept of collusion resilience for addressing (P2), and compare it to existing formalizations of property (P2).
In [19], strong resilience and practicality were used to model the no deviation property of (P2): We identify unwanted properties of strong resilience and we thus investigate variations of it. Specifically, we show that strong Nash Equilibria do not imply strong resilience nor vice-versa (Lemma III.1), and therefore define the collusion resilience property of a joint strategy. Intuitively, collusion resilience considers the sum of the utilities of the deviating parties, since rational players may collude or be controlled by the same entity.
Definition III.8
(Collusion Resilience - CR). A joint strategy \sigma\in\mathscr{S}in an EFG/NFG\ \Gammais called collusion resilient (CR) if no strict subgroup of players S:=\{s_{1}, \ldots,s_{j}\}has a joint incentive in deviating from \sigma. That is , \begin{align*}\forall S \subset N \quad & \forall \sigma_{s_{i}}^{\prime} \in \mathscr{S}_{s_{i}}:\\& \sum\limits_{p \in S} u_{p}(\sigma) \geq \sum\limits_{p \in S} u_{p}(\sigma[\sigma_{s_{1}}^{\prime} / \sigma_{s_{1}}, \ldots, \sigma_{s_{j}}^{\prime} / \sigma_{s_{j}}]). \tag{7}\end{align*}
In addition, we also consider a slight adaption of strong resilience, \mathsf{SR}_{\subseteq}, where the deviation of the entire set of players N is also allowed, as it is for sNE.
Definition III.9 (Strong Subset Resilience - \mathsf{SR}_{\subseteq})
A joint strategy \sigma\in \mathscr{S}is called strongly subset resilient (\mathsf{SR}_{\subseteq}), if no player of any subgroup S\subseteq N, S:=\{s_{1},\ldots,s_{j}\}has an incentive to deviate from \sigma: \begin{align*}\forall S \subseteq N \quad & \forall \sigma_{s_{i}}^{\prime} \in \mathscr{S}_{s_{i}} \quad \forall p \in S:\\& u_{p}(\sigma) \geq u_{p}(\sigma[\sigma_{s_{1}}^{\prime} / \sigma_{s_{1}}, \ldots, \sigma_{s_{j}}^{\prime} / \sigma_{s_{j}}]). \tag{8}\end{align*}
We now formalize how the resilience properties relate to each other, which motivates our definition of (P2).
Lemma III.1 (Resilience Properties)
Let \sigma\in \mathscr{S}be a joint strategy. The following and only the following implications hold .

The next example further motivates why we decided to formalize (P2) in terms of collusion resilience .
Example III.5
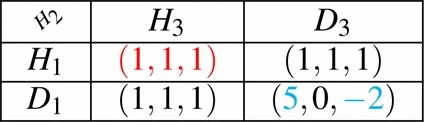
Consider the games \Gamma_{1} and \Gamma_{2}, respectively defined in Tables IV–V. The games \Gamma_{1} and \Gamma_{2}show that there exist cases where both strong resilience and strong Nash Equilibria fail to correctly state whether rational players will deviate, while collusion resilience does not .
Let us study \Gamma_{1}first. There are three players P_{1}on the left , P_{2}in the “3rd dimension” who only has one possible strategy, and P_{3}at the top. Let us consider the joint strategy \sigma=(H_{1},H_{2},H_{3}). Since P_{2}does not have another choice , P_{2}can never deviate. Player P_{1}deviating alone yields the same utility as \sigmaand is thus irrelevant. The same holds for P_{3}. The only deviation that makes a difference, is if P_{1} and P_{3}change strategy together to (D_{1},H_{2},D_{3}). By doing so , P_{1}profits and receives 5 instead of 1, but P_{3}looses by getting -2 instead of 1. Thus , P_{3}does not have an incentive to do so, unless the two players collude for their mutual benefit and share their payoffs. This way they receive 1.5 each instead of 1 each, which poses a serious thread to \sigmaand should thus not be considered satisfying (P2). However , (H_{1},H_{2},H_{3}) is sNEsince P_{3}has no incentive in deviating with P_{1}, if their utilities are not shared, but it is not CRsince \begin{align*}2 & = u_{P_{1}}(H_{1}, H_{2}, H_{3})+ u_{P_{3}}(H_{1}, H_{2}, H_{3}) \tag{9}\\ & < u_{P_{1}}(D_{1}, H_{2}, D_{3})+ u_{P_{3}}(D_{1}, H_{2}, D_{3})=3. \tag{10}\end{align*}
In the similar game \Gamma_{2}, on the contrary , P_{3}has no incentive in deviating from \sigma=(H_{1},H_{2},H_{3})together with P_{1}, also if their utilities are shared. Such a deviation yields 0.5 each, instead of 1 each in \sigma. Hence, there is no incentive to change strategy for one or more players and therefore (H_{1},H_{2},H_{3})should be considered satisfying (P2). Nevertheless, according to Definition II.5, (H_{1},H_{2},H_{3})is not SRsince at least one of the deviating parties P_{1}, P_{3}profits from choosing (D_{1},H_{2},D_{3}), although P_{3}has no reason to play along. However, in \Gamma_{2},(H_{1},H_{2},H_{3}) is CRas \begin{align*}2 & = u_{P_{1}}(H_{1}, H_{2}, H_{3})+ u_{P_{3}}(H_{1}, H_{2}, H_{3}) \tag{11}\\ & \geq u_{P_{1}}(D_{1}, H_{2}, D_{3})+ u_{P_{3}}(D_{1}, H_{2}, D_{3})=1. \tag{12}\end{align*}

Remark 1 (Formalizing ((P1) and (P1))
Based on the re- silience properties of Lemma III.1 we say (P2) is satisfied by a joint strategy \sigma, if \sigma is CRand practical. In addition , ajoint strategy \sigma satisfies (P1), if \sigma is weak immune, as in [19] .
We conclude this section by defining secure game strategies/histories, as follows.
Definition III.10 (Secure Strategy)
A strategy \sigmaof an NFG/EFG is secure if it is weak immune, practical and CR
When discussing security in the setting of EFGs, we are interested mainly in assessing whether a history is secure, as the protocol only defines an honest history instead of a full strategy. By applying Definition III.5, we state the following security characterization.
Definition III.11 (Secure History)
A terminal history \betaof an EFG is secure if there exist extended strategies \sigma_{1}, \sigma_{2}, and \sigma_{3}of \beta, such that \sigma_{1}is weak immune , \sigma_{2}is practical and \sigma_{3} is CR
We note that we do not have to find a secure extended strategy for the history to be secure, as aiming for one joint secure strategy in an EFG would be unnecessarily restrictive. Instead, our goal is to make sure that rational parties follow the honest history, no matter what their actual strategy is. In particular, an honest player follows the honest history by default, a rational player does so because of practicality and collusion resistance. Weak immunity further ensures that honest players as well as rational one cannot be damaged by Byzantine players while following the honest history. Hence, the strategy each player has in mind does not matter, since in a secure protocol weak immune, practical, and collusion resistant, strategies are overlapping along the honest history. This is the case because in Definition III.11 we require \sigma_{1},\sigma_{2}, and \sigma_{3} to all yield the same history, namely \beta. We can therefore admit that an honest player has a weak immune strategy in mind, while a rational player has a practical one, as long as these overlap on the honest history.
IV. Closing Games of Off-Chain Protocols
We now define a new two-player EFG, called the Closing Game G_{c}, in order to model closing phase properties of off-chain protocols, in particular of the Lightning Network. As explained in Section II-A, to close a channel a party can unilaterally publish a channel state on-chain, which does not necessarily have to be the latest one. The one who closes, however, has to wait a certain amount of time until the money can be used. Meanwhile, the other party can steal all the money from the channel in case the state published on-chain is not the latest one: this ensures that rational players close their channel only with the latest state. Alternatively, the parties can collaboratively sign a new transaction to split the money. In this case no one has to wait.
Our closing game overcomes the limitations of previous work [19] in representing dishonest closing attempts, by modeling how closing can be achieved after a failed collaborative closing attempt and by also considering the additional fee f to be paid in a revocation transaction.
To the best of our knowledge, our closing game G_{c} is the most accurate model for the security analysis of off-chain protocols, notably of the Lightning Network. In our model of the closing phase we make the following assumptions for a channel between A and B at the moment where the closing phase is initiated.
- The fair split of the channel's funds is a\rightarrow A, b\rightarrow B and a > 0, b > 0.
- The benefit of closing the channel is \alpha. Closing a channel yields a benefit, since it unlocks assets.
- The opportunity cost of having to wait for one's funds upon closing is \varepsilon.
- When both players agree to update the channel we assume a fair deal in the background which yields a profit of \rho for both parties.
- Publishing a revocation transaction on-chain costs a fee f > 0.
Further, to properly model utilities in the closing game G_{c}, we define the following total order, which is crucial for analyzing security properties of G_{c}. For capturing total order properties in the setting of G_{c}, we extend the set \mathbb{R} of real numbers by the infinitesimal numbers \alpha,\ \varepsilon and \rho.
Definition IV.1 (Utility Order)
We consider the total order (\mathbb{U},\preccurlyeq), where \mathbb{U}is the group resulting from closing \mathbb{R}\dot{\cup}\{\alpha,\varepsilon,\rho\}under addition. The total ordering \preccurlyeq isuniquely defined by the following conditions .
- On \mathbb{R}, the relation \preccurlyeq isthe usual less than or equal relation \preccurlyeq\vert _{\mathbb{R}}:=\leq.
- The values \alpha,\ \varepsilon and \rhoare greater than 0, \begin{equation*}\forall\xi\in\{\alpha,\varepsilon,\rho\}:-\xi\prec 0\prec\xi. \tag{13}\end{equation*}
- The values \alpha,\ \varepsilon and \rhoare closer to 0 than any real number , \begin{equation*}\forall x\in \mathbb{R},\xi\in\{\alpha,\varepsilon,\rho\},x > 0:\xi\prec x, -x\prec-\xi. \tag{14}\end{equation*}
- Additionally , \alpha,\ \varepsilon and \rhohave the order \rho\prec\varepsilon\prec\alpha.
In general, unlocking funds gives additional financial freedom even if there is some processing delay; therefore, we choose \varepsilon\prec\alpha in Definition IV.1. Additionally, once the parties initiate the closing phase, it is reasonable to assume that no potential update significantly benefits both parties. In contrast, both parties are interested in avoiding the opportunity cost, i.e., the cost of having to wait for their funds upon closing, therefore, we set \rho\prec\varepsilon in Definition IV.1.

Remark 2
While the ordering conditions of Definition IV.1 may seem to be restrictive, lifting them comes with the burden of considering a high number of possible variable orderings. In particular, one would need to consider (number of variables)! orderings, which would highly complicate the formal analysis task. Approximating or clustering the number of orderings, while weakening conditions in Definition IV.1, is an interesting venue for future work .
Based on the utility ordering of Definition IV.1, we introduce our Closing Game for Player A below.
Definition IV.2 (Closing Game G_{c}(A) of Player A)
The Clos- ing Game G_{c}(A)=(N,\mathscr{H},P,u)is an EFG with two players N=\{A,B\}. The tree representation of G_{c}(A)in Figure 4 defines \mathscr{H},\ P and u^{3}with the actions of the game being summarized in Table VI .
Note that the utility function u of G_{c}(A) in Figure 4 assigns player p\in N the money player p received minus the money player p deserved based on the latest channel state. The values of closing (\alpha), updating (\rho) and waiting (-\varepsilon) are also considered in Figure 4. As discussed in Section II-A, the fee needed for the closing transaction is assumed to have been reserved among the locked funds in the channel all the time and is spent upon closing, therefore not affecting the players' channel balance.
The closing game for player B,\ G_{c}(B) is defined similarly to G_{c}(A), with the roles of A and B being swapped in Definition IV.2. Based on the closing games G_{c}(A) and G_{c}(B), we consider the closing phase in an off-chain channel as given in Figure 5 and defined below.
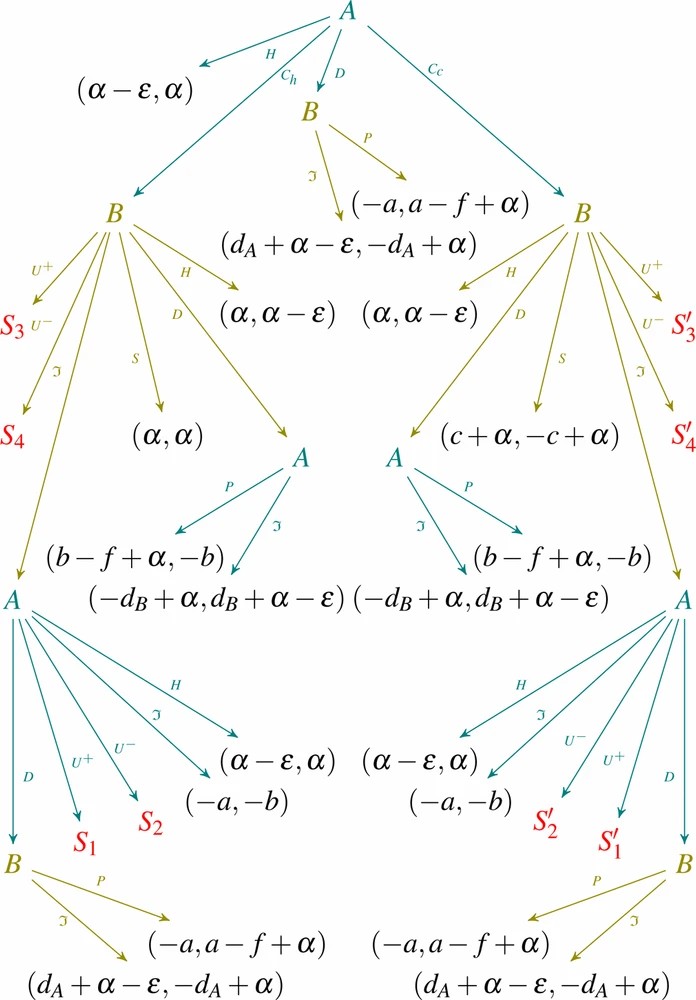
Fig. 4.Fig. 4. Closing game G_{c}(A).
Definition IV.3 (Closing Phase)
The closing phase of an off- chain channel modeled by a closing game G_{c}(A)is initiated in one of three ways: (i) A starts with a closing action C, and thus triggers the closing game G_{c}(A);\ (ii)\ Adoes not start a closing action, thus performing action ignore \Im, but Bstarts with a closing action Cand triggers G_{c}(B); or (iii) none of the players A and Bever start closing, that is Balso choosing action \Im, in which case the money stays locked in the channel. Then, we get the EFG\ \Gamma_{C}from Figure 5 modeling the closing phase of G_{c}(A) and G_{c}(B).
V. Closing Games for Secure Lightning Channels
We now show that the closing games from Definition IV.2 precisely capture secure closing phases in Lightning channels [6]. Namely, the following two terminal histories of closing games model the honest behavior of Lightning: (i) history (H) from Figure 4 represents unilateral honest closing of A, yielding utility (\alpha-\varepsilon, \alpha); and (ii) history (C_{h},S) captures the attempt of A to close collaboratively and honestly, while B signs, with a utility of (\alpha, \alpha). Our security analysis focuses on these two honest histories of Lightning channels.3
Fig. 5.Fig. 5. Closing phase \Gamma_{C}.
Definition V.1 (Honest Closing)
The only honest histories in the closing game G_{c}(A)are the terminal histories (H)honest unilateral closing and (C_{h},S)honest collaborative closing. All strategies yielding one of the two histories are considered honest strategies.
In the following, the values d_{A} (resp. d_{B}) defined in Table VI (line D) represent the difference of funds between the latest state and the old one that is dishonestly posted on chain by A (resp. B). In other words, if (a,b) is the latest state, the one posted on chain is (a+d_{A},b-d_{A}) (resp. (a-d_{B},b+d_{B})), thus enabling dishonest closing attempts of profit d_{A} for A (resp. d_{B} for B). The values p_{A,B} (Table VI, lines U^{+}, U^{-}) and c (Table VI, line C_{c}) can respectively be chosen by A and B at the time of the action and do not depend on previous distribution states. Based on this setting, we derive the security properties (P1) and (P2) of Lightning channels as given below. The omitted proofs are given in [39].
Theorem V.1
(Weak Immunity of Honest Behavior - (P1)). The terminal histories (H)of honest unilateral closing, and (C_{h},S)of honest collaborative closing of G_{c}(A)are weak immune, if the channel balances are higher than the fee required in a revocation transaction, that is if a\geq f and b\geq f
Theorem V.1 implies that as long as both players have a minimal balance of f in the channel, no honest player can lose money. As such, Theorem V.1 establishes the security property (P1) ensuring “no honest loss” in the channel.
Further, to ensure the security property (P2) of “no deviation”, we require that \begin{align*}&a- p_{B}+ d_{A}\geq f\ \ \text{and} \tag{15}\\ &b- p_{A}+ d_{B}\geq f. \tag{16}\end{align*}
To understand the in equations (15)–(16) consider the history (C_{h}, \mathfrak{I}, U^{-}, \mathfrak{A}, D) in Figure 4, respectively S_{1}^{\prime}. This history formalizes the case where A attempts honest collaborative closing (action C_{h}) and B ignores it (action \Im). Then A proposes an update (action U^{-}) from state (a,b) to state (a-p_{B},b+p_{B}) and B agrees (action \mathfrak{A}). Finally, A closes dishonestly (action D) using the old distribution state (a-p_{B}+d_{A},b+p_{B}-d_{A}). Let us also study the options B has. By ignoring A^{\prime}\mathrm{s} behavior (action \Im), B receives b+p_{B}-d_{A} instead of the fair amount b+p_{B}, leaving B with a loss of d_{A}. By publishing the revocation transaction (action P), B receives a+b but has to pay the fee f for pushing it on the blockchain, which leads to a win of a-p_{B}-f. Therefore, the win should be greater than the loss; hence \begin{equation*}a-p_{B}-f\geq-d_{A}\quad \Leftrightarrow\quad a-p_{B}+d_{A}\geq f, \tag{17}\end{equation*} in order for a rational B to publish the revocation transaction.
This in turn yields a loss for A and hence discourages A from closing dishonestly, which is necessary for the incentive compatibility (P2) of Lightning's closing phase. By swapping A^{\prime}\mathrm{s} and B^{\prime}\mathrm{s} roles, we get the prerequisite formulated in (16). These extreme cases of dishonest closing subsume the others. Thus, the only preconditions we need in the following Theorem V.2 are (15)-(16). In summary, formulas (15)–(16) ensure that ignoring any dishonest closing attempt is worse than publishing the revocation transaction. Property (P2) is then established by the following theorem.
Theorem V.2 (Incentive-Compatibility - (P2))
If a-p_{B}+ d_{A}\geq f and b-p_{A}+d_{B}\geq f, then
- honest unilateral closing (H) is CRbut not practical .
- honest collaborative closing (C_{h},S) is CR, It is practical iff c\neq p_{A}.
Remark 3 (Explanation of c\neq p_{A})
The condition c\neq p_{A}in Theorem V.2 has the following relevance. Player Acan in principle choose to propose dishonest collaborative closing (action C_{c}), providing Aan unfair advantage of value c. Then, either B (action U^{+}) or A\ (Bchoosing action \Imto ignore first, then Ataking action U^{+}) can propose a channel update (a,b)\mapsto(a+c,b-c). The value of the update p_{A}is now equal to the amount player A cheated with in C_{c}:\ p_{A}=cIn this special case, the closing game behaves differently. The described histories (C_{c},\Im, U^{+}) and (C_{c},U^{+})lead to the subgames S_{1}^{\prime} and S_{3}^{\prime}respectively. Let us consider S_{3}^{\prime}with p_{A}=c.
Assume Aagrees to the update, action \mathfrak{A}, and player Bsigns the initially unfair collaborative closing attempt of A. Since in the meantime the channel was updated by the exact amount that Atried to cheat with, the pending collaborative closing now contains the fair split. Therefore, both players profit from this course of action, yielding utility (\rho+\alpha,\rho+\alpha). The analog can be achieved in subgame S_{1}^{\prime}with the history (\mathfrak{A},\Im,S). In fact, for p_{A}=c, those histories are the only practical ones and provide the mutually best outcome possible .
However, updating to (a+c,b-c)first and then closing honestly and collaboratively yields the exact same result. This is why we study the closing game without the possibility of updating after a closing attempt in the next section Section V-A .
We now state our first main security theorem. Since (H) is not practical, a rational player will not play it. Hence, the terminal history (H) is not secure. We get the following security result instead for (C_{h},S).
Theorem V.3 (Security of G_{c}(A))
If a\geq f,\ b\geq f,\ a-p_{B}+ d_{A}\geq f, b-p_{A}+d_{B}\geq f, and c\neq p_{A}, then the closing game G_{c}(A)together with the honest behavior (C_{h},S) is secure.
Proof
As a\geq f and b\geq f, we have that (C_{h},S) is weak immune (Theorem V.1. Since a-p_{B}+d_{A}\geq f, we derive b-p_{A}+d_{B}\geq f and c\neq p_{A}, we have that (C_{h},S) is also practical and CR (Theorem V.2). Hence, by Definition III.11,(C_{h},S) is secure.
Theorem V.2 implies that for honest and rational players the action of collaborative closing followed by signing (C_{h},S) is the best way to close an off-chain channel. It also implies, that rational adversaries will cooperate. Further, Byzantine players represent no threat as long as their channel balances are high enough and they do not engage in special cases of channel updates after a collaborative closing attempt.
We note that for proving our security properties (P1)-(P2) in Theorem V.1–Theorem V.3, we rely on a succinct analysis of the finite graph properties of the closing game G_{C}(A) from Figure 4. While automated approaches analyzing a finite number of graph properties exist, see e.g. [43],[44], these approaches cannot handle (game) graphs where graph leaves contain variables, instead of specific numerical values, which is the case of G_{C}(A). For such cases, automated reasoning tools, such as theorem provers, need to be combined with graph-theoretic manipulations of G_{C}(A), an approach we aim to investigate as a future work towards automating the security analysis (and proofs) of closing games.
A. Closing Games Without Updates
We will now consider a variation of closing games without updates, as updating is not beneficial for at least one player upon closing. Furthermore, we avoid special cases such as the one described in Remark 3, which should be equivalent to updating before initiating G_{c}(A), and then closing honestly and collaboratively. As such, the closing game G_{c}(A)without updates results from removing all actions U^{+} and U^{-} in Figure 4. For the resulting closing game G_{c}(A) without updates we get the following security result similar to Theorem V.3.
Theorem V.4 (Security of G_{c}(A) without Updates)
If a\geq f and b\geq f, then the closing game G_{c}(A)without updates and together with both honest histories (H) and (C_{h},S) is secure.
Proof
We respectively fix honest strategies \sigma and \sigma^{\prime} for histories (H) and (C_{h},S); let \sigma^{\prime} have A choosing C_{h} initially, P after (C_{h},D) and H after (C_{h},\Im), and then B choosing S after (C_{h}), P after (D) and H after (C_{c}). Infer that the deviation of A causes negative utility for B, whereas the deviation of B leads to non-negative utility for A as b-f\geq 0. By Theorem V.1 we thus have that \sigma^{\prime}, and therefore (C_{h},S), are weak immune. In addition, Theorem V.1 implies that also (H) is weak immune.
To show practicality, we compute all subgame perfect terminal histories. From a\geq f and b\geq f we have a+d_{A}\geq f and b+d_{B}\geq f. Since closing with a dishonest behavior yields utility a-f+\alpha,\ b-f+\alpha respectively, whereas ignoring a dishonest behavior leads to -d_{A}+\alpha and -d_{B}+\alpha, we conclude that the best choice after action D is always P. Thus, A^{\prime}\mathrm{s} best choice after (C_{h},\Im) and (C_{c},\Im) is H. Therefore, B has the two subgame perfect options \Im and S after (C_{h}), and only \Im after (C_{c}), yielding thus the following practical histories: history (C_{h},S) with utility (\alpha, \alpha); and (C_{h},\Im,H), (C_{c},\Im,H), and (H) each with utility (\alpha-\varepsilon,\alpha). Therefore, both (H) and (C_{h},S) are practical.
Note that every practical terminal history is a Nash Equilibriurn, since if a deviation could benefit a player, the player would have chosen differently already. As CR is equivalent to Nash Equilibria in two-player games (by Definition II.5 and Lemma III.1), we use Definition III.7 and Lemma III.1 to conclude that practicality of (H) and (C_{h},S) implies collusion resistance CR of (H) and (C_{h},S). As (H) and (C_{h},S) are both weak immune, practical and CR, by Definition III.11 we infer that they are also secure.
Remark 4
Note that the analysis of utilities in the closing game G_{c}(A)crucially depends on constraints of the underlining ordering that we set in Definition IV.1 and thus on the values of variables a,b,c,d_{A,B},fin Table V.I. In general, the bigger \varepsilongets in Definition IV.1 the more discouraged is closing unilaterally in Table VI, and hence in Figure 4. Further , Bis more likely to accept a dishonest collaborative closing attempt C_{c}, as it is better to lose cthan to lose \varepsilon.
We further study what happens if a player has almost no funds left in a channel. In particular, we show that security properties, in particular weak immunity and practicality, are violated in this case, thereby formalizing the following folklore in the community.
Theorem V.5 (Little Funds)
If a < f, then only terminal histories that involve an explicit cheating attempt are weak immune in the closing game G_{c}(A)without updates. A terminal history involves an explicit cheating attempts if one of its actions is C_{c}or D.
Proof
Let \sigma be any strategy, yielding a history that does not involve an explicit cheating attempt. Then A can deviate to a strategy where A chooses D as its first action. In this case, the honest B gets negative utility, no matter whether B chooses P or \Im, since a < f. Hence, only histories that involve explicit cheating attempts can be weak immune.
We next derive the following results on security properties.
Corollary 1
If there exists an old channel state (a+d_{A},b- d_{A}), with a+d_{A} < f, then neither history (H)nor (C_{h},S)is weak immune nor practical, but CR
Corollary 2
Arational party should never, in any channel , let the opponent's balance fall below f, because at that point the other party can always cause financial loss by closing dishonestly and unilaterally44 The special edge cases a=0 or b=0 are considered in [39]. .
Proof
Once the opponent's balance is below f, that party can start the closing game, therefore the opponent becoming A. Thus, by applying Theorem V.5, it follows that the opponent can make the rational player lose money by closing unilaterally and dishonestly. If it is not the first time that A^{\prime}\mathrm{s} balance is below f and the respective old state contains a higher balance for A than the latest one, then we are even in the situation of Corollary 1. It is thus rational of A (practical) to close dishonestly.
B. Optimal Strategy for Closing Off-Chain
To summarize, our security analysis based on closing games for Lightning channels yields the following results. Theorem V.4–Theorem V.5, together with with Corollary 1–Corollary 2, allow us to derive the optimal strategy for closing an off-chain channel for a rational and suspicious player. We next describe and illustrate this optimal strategy, highlighting the main steps of our security analysis based on Theorem V.2–Theorem V.5.
Without loss of generality, we assume the current state of the channel is (a,b).
The player, assumed to be player A, who initiated the closing phase shall:
- try to close honestly and collaboratively (action C_{h}), if there does not exist an old state (a+d_{A},b-d_{A}), where d_{A} > 0 and a+d_{A} < 0. In case the other player, that is player B, does not sign (action S), player A shall close honestly and unilaterally (action H). If player B closed dishonestly and unilaterally (action D), player A shall:
- state the revocation transaction (action P), if the state used for cheating was (a-d_{B},b+d_{B}), where d_{B} > 0 and b+d_{B}\geq f.
- ignore the cheating otherwise (action \Im), as it yields less loss.
- close dishonestly and unilaterally (action D), if there exists an old state (a+d_{A},b-d_{A}), where d_{A} > 0 and a+d_{A} < f. In this case, player A shall use the old distribution state (a+d_{A}^{\prime},b-d_{A}), with the highest d_{A}^{\prime} > 0 that still satisfies a+d_{A}^{\prime} < f.
The reacting player, in this case assumed to be player B, shall:
- sign the collaborative honest closing attempt (action S), if applicable, if there is no old state (a-d_{B},b+d_{B}), d_{B} > 0 in which the funds of player B are less then f, that is if b+d_{B} < f.
- close honestly and unilaterally (action H), in case of a dishonest collaborative closing attempt (action C_{c}). This holds, if there is no old state (a-d_{B},b+d_{B}),\ d_{B} > 0 in which the player B^{\prime}\mathrm{s} funds are less then f, that is b+d_{B} < f.
- otherwise ignore (action \Im) the collaborative and honest/dishonest closing attempt, if applicable, and close dishonestly and unilaterally (action D), using the old state (a-d_{B}^{\prime},b+d_{B}^{\prime}), with the highest d_{B}^{\prime} > 0 that still satisfies b+d_{B}^{\prime} < f.
- state the revocation transaction (action P), if player A tried to close dishonestly and unilaterally (action D) with state (a+d_{A},b-d_{A}), where d_{A} > 0 and a+d_{A}\geq f. • ignore (action \Im) if player A closed dishonestly (action D), in the case where a+d_{A} < f, as it yields less loss.
Example V.1
Let players A and Bshare a channel with initial balance (5,5) and let us assume the fee for publishing a revocation transaction f=2. After the first update let their state be (3,7). The optimal way for Ato close now is C_{h}and for Bto sign. Dishonest closing would cause Bto publish the revocation transaction, yielding a loss of 3 for Aand a profit of 3-2=1for B.
The next update could be (1.8,8.2). The best way to close for Ais still C_{h}. Dishonest closing using (3,7), for example, would still cause Bto publish the revocation transaction. Player Bwould in this case lose 1.8-2=-0.2, but he would lose more , 7-8.2=-1.2, by ignoring it .
Another update could be (1,9). Now the optimal strategy for Ato close is D, using the old state (1.8,8.2). Ignoring the dishonest closing (action \Im) brings B-0.8, but proving A^{\prime}scheating (action P) leads to 1-2=-1. Hence, a rational Bwill choose to ignore (action \Im), that means Bdoes not publish the revocation transaction .
VI. Beyond Closing Games for Off-Chain Security
Our game-theoretic analysis so far focused on using closing games to capture security properties of off-chain channels (Section IV), and in particular of Lightning channels (Section V). In this section, we show that our game-theoretic formalism from Section III is expressive enough to analyse more complex protocols than just closing phases in Lightning channels. In particular, we introduce a new EFG, called the Routing Game in Section VI-A, and use this game in Section VI-B to disprove security of Lightning's routing mechanism amid the Wormhole and Griefing attacks [7],[20]. We also discuss a natural extension of our analysis to model other off-chain protocols in Section VI-C.
A. Routing Games for Lightning's Routing Module
We first propose a new EFG, called the Routing Game , showing that EFGs can capture actual attacks, in this case the Wormhole attack [7] and the Griefing attack [20], which were overlooked for example in [19]. Specifically, the below defined routing game considers fees f , and supports actions allowing the intermediaries to choose not to claim their money using the secret x but instead to forward it to another intermediary (as explained in Section II-A). Additionally, other deviations such as creating a conditional payment (i.e. HTLC) with a different hash value, a different amount, or a different time-out than expected are also considered. For simplicity, we chose to model our routing game below with five players; however, an arbitrary number of intermediaries can be modeled.
Definition VI.1 (Routing Game G_{\text{rout}})
The routing game G_{rout}=(N_{r},\mathscr{H}_{r},P_{r},u_{r})is an EFGwith five players N= \{A,E_{1},I,E_{2},B\}, where
- the histories \mathscr{H}_{r}, the next player function P_{r}, and the utility function u_{r}are defined via the tree representation of Figure 6. The utility tuples in Figure 6 assign the first value to A, the second to E_{1}, the third to I, the fourth to E_{2}, and the last to B;
- the actions of G_{rout}are as listed in Table VII .
We note that our Routing Game G_{\text{rout}} has four types of subgames, as modeled in Figure 6 and described next: (i) subgames that result from sending the secret to another player
\mathfrak{S}_{i}; (ii) subgames that result from locking a wrong amount of money in the HTLC \mathbb{S}_{i}; (iii) subgames that result from using a wrong time-out in an HTLC \mathbf{S}_{i}; and (iv) subgames that result from using a wrong hash value as lock in the HTLC
\mathsf{S}_{i}. We further note that Figure 6 only gives a partial model, as not all subgames are presented in Figure 6. However, within one type of subgame, the game trees are similar. Therefore, we provide
only one instance of each type in [39], which are the subgames \mathbb{S}_{1},\ \mathsf{S}_{2}, and \mathbf{S}_{3}. An instance of a secret forwarding subgame capturing the Wormhole attack can be
seen in G_{\text{rout}}, as the subtree after history (S_{H},L,L,L,L, U,S_{S_{E_{1}}}).
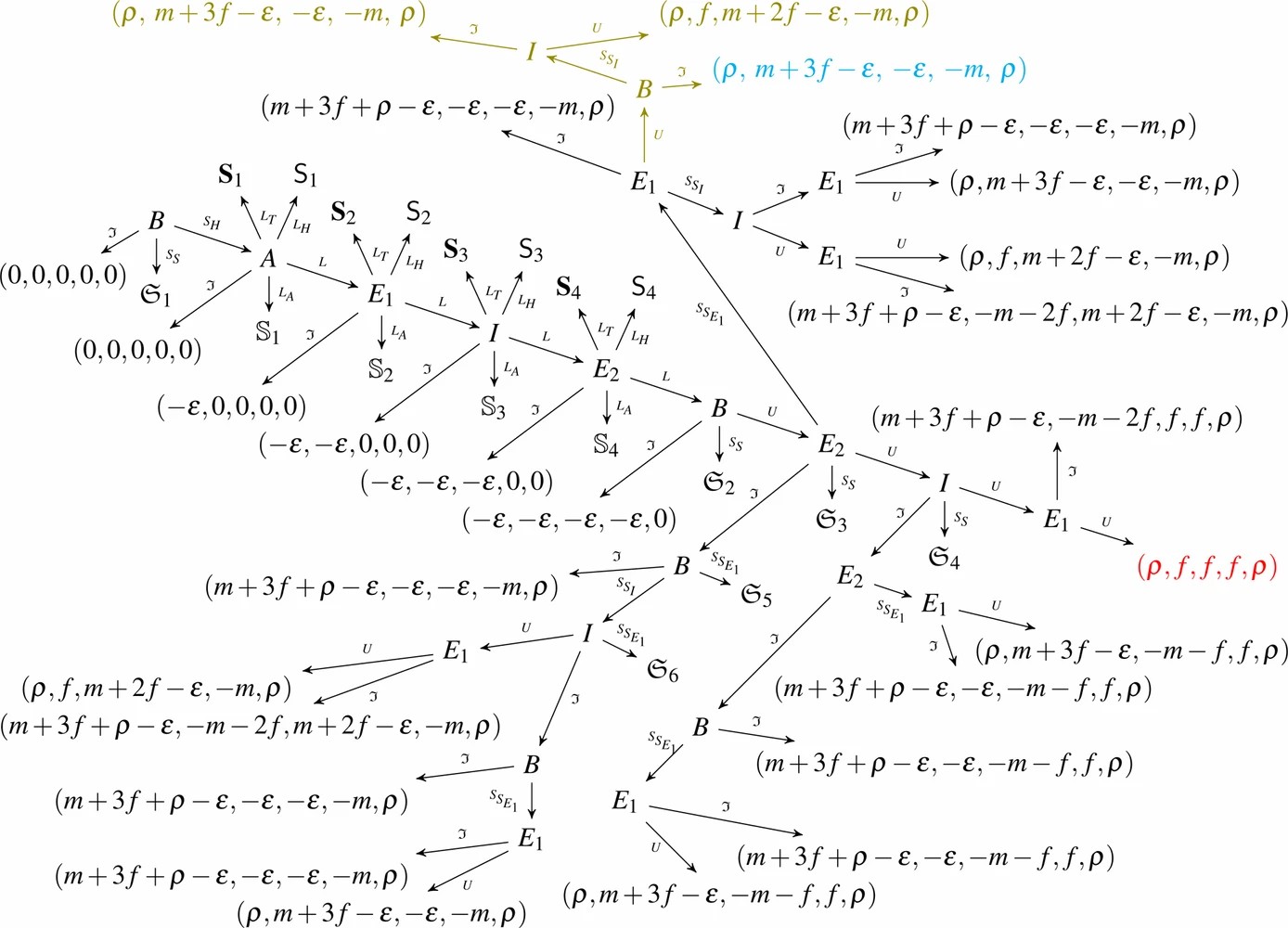
Fig. 6.Fig. 6. Partial definition of the lightning's routing G_{\text{rout}} and the Fulgor Model G_{\text{Ful}}. The olive colored subtree only applies for G_{\text{rout}}.
Let us emphasize that the utility function u_{r} of G_{\text{rout}} assigns each player p\in N the relative profit of their routing actions and does not mirror the individual channel balances. It also takes the value \rho of a successful payment and the opportunity cost \varepsilon into account.
As in the closing games G_{c}(A) and G_{c}(B), we aim to align utility and monetary outcome as tight as possible. We adjust the ordering (\mathbb{U},\preccurlyeq) of Definition IV.1 by not assuming that \rho\prec\varepsilon, since achieving an update is the ultimate goal of the routing protocol. We also consider the utility relative to the amount due to each party.
B. Security Analysis of Lightning's Routing Module
Let us recall Figure 1 and Figure 2, where player A wants to pay another player B money of value m. Since, A and B do not share a channel, the three intermediaries E_{1},\ I, and E_{2} support the payment, with each receiving a fee f > 0 for their collaboration if the payment is successful. Each player who creates an HTLC locks her money for a given time, yielding an opportunity cost of \varepsilon if the money is returned. If the transaction fails, before anyone has unlocked an HTLC, all parties get utility 0 or -\varepsilon, depending on whether they created an HTLC or not. Otherwise, the intermediaries' utilities are according to their financial win/loss. The parties A and B both receive \rho once B is paid. Should the transaction fail after B is paid, but before A has paid, she has utility m+3f+\rho-\varepsilon; once E_{1} collects the money, A^{\prime}\mathrm{s} utility is \rho.
In the sequel, we consider the behavior from Figure 1 as the only honest history in G_{\text{rout}}, as also formalized next.
Definition VI.2 (Honest Routing)
The only honest history in the routing game G_{rout}is the history (S_{H},L,L,L,L,U,U,U,U). All strategies yielding this history are considered honest strategies.
Using our model G_{\text{rout}} and its honest behavior, we derive the following result.
Theorem VI.1
(Vulnerability of G_{\text{rout}} to Wormhole Attacks). The honest behavior (S_{H},L,L,L,L,U,U,U,U)of the Routing Game G_{rout}is not CR
Proof
The utility of the honest behavior of the routing module (S_{H},L,L,L,L,U,U,U,U) is (\rho,f,f,f,\rho) (as indicated in red in Figure 6). Let us compare this behavior and utility to the deviating terminal history (S_{H},L,L,L,L,U,S_{S_{E_{1}}}, U,\Im) with a utility of (\rho,\ m+3f-\varepsilon,\ -\varepsilon, -m,\ \rho) (given in blue in Figure 6). It is not hard to argue that the collusion of E_{1} and E_{2} (and B by not sending the secret to I) strictly profits from the deviation, which yields a joint utility of 3f-\varepsilon+\rho, whereas the honest behavior only yields a joint utility of 2f+\rho. As such, collusion resistance CR is violated, since no honest player can prevent the Wormhole attack from happening by following any honest strategy (that is, a strategy \sigma whose history is the honest behavior (S_{H},L,L,L,L,U,U,U,U)).
In conclusion, Theorem VI.1 formally proves that Lightning's routing module is susceptible to the Wormhole attack. We further extend this result by noting that not only can G_{\text{rout}} capture the Wormhole attack, but also the Griefing attack, as stated below.
Theorem VI.2 (Vulnerability of G_{\text{rout}} to Griefing Attack)
The honest behavior (S_{H},L,L,L,L,U,U,U,U)of the Routing Game G_{rout}is not weak immune .
Proof
For showing that history (S_{H},L,L,L,L,U,U,U,U) is not weak immune, we prove that no strategy which yields this history is weak immune. Let us consider any such strategy \sigma. Then, player A has to choose action L after B sent her the secret, that is history (S_{H}). Assume now E_{1} deviates and chooses to ignore (action \Im). Then A's utility is -\varepsilon\prec 0. Hence, history (S_{H},L,L,L,L,U,U,U,U) is not weak immune.
We also obtain the following result as an immediate consequence of Theorem VI.1 and Theorem VI.2.
Corollary 3
(Security of Routing Module). The honest be- havior (S_{H},L,L,L,L,U,U,U,U)of the Routing Game G_{rout}is not secure. Hence, the Routing Game G_{rout}is not secure .

Fig. 7.Fig. 7. Routing in fulgor.

C. Further Routing Protocols Beyond the Lightning Network
We conclude this paper by arguing that our EFG games, either closing or routing games, are not restricted to Lightning networks but can be used for other protocols as well. In the remaining of this section, we illustrate how to model Fulgor [38], a payment channel network protocol that fixes the Wormhole attack, but not the Griefing attack.
The routing mechanisms used in Fulgor is similar to Lightning's routing, and is similarly based on HTLCs. The main difference lies in the structure of the secrets and their hashes. Indeed, while Lightning uses the same secret x for every HTLC, Fulgor provides a different secret and hash lock for each player.
Fulgor's routing mechanism is illustrated in Figure 7, where player A generates different secrets and hash locks at the beginning. The secrets and the hashes relate in the following way: h(x_{1})=y_{1},\ h(x_{1}+x_{2})=y_{2},\ h(x_{1}+x_{2}+x_{3})=y_{3} and h(x_{1}+x_{2}+x_{3}+x_{4})=y_{4}. Therefore, a player only gets to know a sum of secrets when the right-hand party unlocks and subtracts the secret value received from A to unlock their HTLC. A also provides a zero-knowledge-proof \text{ZKP}_{i} for each intermediary [45] to prove that the secrets and hashes constructed this way guarantee successful unlocking of the left HTLC, which is essential to not lose funds.
The game-theoretical (EFG) model of Fulgor G_{Ful} reported in Figure 6 looks similar to the routing game G_{\text{rout}}, yet, with one significant difference. Consider the history (S_{H},L,L,L,L,\ U,S_{S_{E_{1}}}) in Figure 6, which enables player E_{1} to unlock (action U) the HTLC created by A. In Fulgor, the same history does not enable E_{1} to unlock the HTLC. As Figure 7 shows, the secrets that E_{2} can share after action 6 are x_{4} and x_{1}+x_{2}+x_{3}+x_{4}. Further, E_{1} only knows x_{2}, thus there is no way to compute x_{1}. This is however the value needed to unlock the HTLC created by A. Indeed, Fulgor is not affected by the Wormhole attack. Nevertheless, similarly to Theorem VI.2, the honest behavior of Fulgor is not weak immune, as it is vulnerable to the Griefing attack.
VII. Conclusions
Our work advocates the use of Extensive Form Games (EFGs) for the game-theoretic security analysis of off-chain protocols. In particular, we introduce two instances of EFGs to model the closing and the routing of the Lightning Network. By doing so, we take the first step towards closing the gap existing security proof techniques have due to using informal arguments about rationality. We express security properties as formal requirements over joint strategies in EFGs, allowing us to establish optimal strategies for closing off-chain and capture security vulnerabilities amid attacks. Given the theoretical expressiveness of our EFGs, future work includes the definitions of new games to capture a wider range of off-chain protocols. To overcome the burden of tedious manual analysis, we also plan to leverage SMT solving and/or automated theorem proving in order to provide automated security proofs.
Footnotes
- 1 We refer the interested reader to [39] for the complete definitions and proofs.
- 2 If the funding transaction is published on-chain before the first commitment transactions are signed, a party may hold the other hostage since none of the parties can close the channel unilaterally but only in collaboration.
- 3 The subgames S_{i}, S_{i}^{\prime} are given in [39].
- 4 The special edge cases a=0 or b=0 are considered in [39].
Acknowledgments
We thank our anonymous reviewers for their valuable feedback. The work was partially supported by the European Research Council (ERC) under the ERC CoG ARTIST 101002685 and the ERC CoG BROWSEC 71527; by the TU Wien Doctoral College SecInt; by the Austrian Science Fund (FWF) projects PROFET P31621 and LogiCS W1255-N23; by the Austrian Research Promotion Agency (FFG) (COMET K1 SBA, COMET K1 ABC); by the Vienna Business Agency project Vienna Cybersecurity and Privacy Research Center (VISP); by the Austrian Federal Ministry for Digital and Economic Affairs; the National Foundation for Research, Technology and Development; and the Christian Doppler Research Association through CDL-BOT.
References
- [1]S. Nakamoto, “Bitcoin: A Peer-to-Peer Electronic Cash System,” https://biicoin.org/bitcoin.pdf, 2008.
- [2]G. Wood, “Ethereum: A SecureDecentralised Generalised Transaction Ledger,” https://gavwood.com/paper.pdf, 2014.
- [3]A. Hafid, A. Senhaji Hafid, and M. Samih, “Scaling Blockchains: A Comprehensive Survey,” IEEE Access, pp. 125244–125262, 2020.
- [4]A. Chauhan, O. Malviya, M. Verma, and T. Singh Mor, “Blockchain and Scalability,” in QRS-C, 2018, pp. 122–128.
- [5]L. Gudgeon, P. Moreno-Sanchez, S. Roos, P. McCorry, and A. Gervais, “SoK: Layer-Two Blockchain Protocols,” in FC, 2020, pp. 201–226.
- [6]J. Poon and T. Dryja, “The Bitcoin Lightning Network: Scalable Off-Chain Instant Payments,” 2016, https://lightning.network/lightning-network-paper.pdf.
- [7]G. Malavolta, P. Moreno-Sanchez, C. Schneidewind, A. Kate, and M. Maffei, “Anonymous Multi-Hop Locks for Blockchain Scalability and Interoperability,” in NDSS, 2019.
- [8]L. Aumayr, O. Ersoy, A. Erwig, S. Faust, K. Hostakova, M. Maffei, P. Moreno-Sanchez, and S. Riahi, “Generalized Channels from Limited Blockchain Scripts and Adaptor Signatures,” in AsiaCrypt, 2021.
- [9]L. Aumayr, M. Maffei, O. Ersoy, A. Erwig, S. Faust, S. Riahi, K. Hostakova, and P. Moreno-Sanchez, “Bitcoin-Compatible Virtual Channels,” in SP, 2021, pp. 901–918.
- [10]L. Aumayr, P. Moreno-Sanchez, A. Kate, and M. Maffei, “Blitz: Secure Multi-Hop Payments Without Two-Phase Commits,” in Usenix Security, 2021, pp. 4043–4060.
- [11]Z. Avarikioti, E. K. Kogias, R. Wattenhofer, and D. Zindros, “Brick: Asynchronous Incentive-Compatible Payment Channels,” in FC, 2021, pp. 209–230.
- [12]C. Decker and R. Wattenhofer, “A Fast and Scalable Payment Network with Bitcoin Duplex Micropayment Channels,” in SSS, 2015, pp. 3–18.
- [13]S. Dziembowski, L. Eckey, S. Faust, and D. Malinowski, “Perun: Virtual Payment Hubs over Cryptocurrencies,” in SP, 2019, pp. 106–123.
- [14]S. Dziembowski, L. Eckey, S. Faust, J. Hesse, and K. Hostáková, “Multi-Party Virtual State Channels,” in EuroCrypt, 2019, pp. 625–656.
- [15]P. McCorry, S. Bakshi, I. Bentov, S. Meiklejohn, and A. Miller, “Pisa: Arbitration Outsourcing for State Channels,” in AFT, 2019, pp. 16–30.
- [16]Z. Avarikioti, O. S. T. Litos, and R. Wattenhofer, “Cerberus Channels: Incentivizing Watchtowers for Bitcoin,” in FC, 2020, pp. 346–366.
- [17]S. A. K. Thyagarajan, G. Malavolta, F. Schmidt, and D. Schröder, “PayMo: Payment Channels For Monero,” IACR Cryptol. ePrint Arch., 2020.
- [18]R. Canetti, Y. Dodis, R. Pass, and S. Walfish, “Universally Composable Security with Global Setup,” in TCC, 2007, pp. 61–85.
- [19]P. Zappalà, M. Belotti, M. Potop-Butucaru, and S. Secci, “Game Theoretical Framework for Analyzing Blockchains Robustness,” IACR Cryptol. ePrint Arch., 2020.
- [20]A. Khosla, E. Schwartz, and A. Hope-Bailie, “Connector Risk Mitigations-Interledger RFCs, 0018,” 2019. [Online]. Available: https://inicrlcdgcr.org/rfcs/0018-conncctor-nsk-mitigations/.
- [21]G. Avarikioti, F. Laufenberg, J. Sliwinski, Y. Wang, and R. Wattenhofer, “Towards Secure and Efficient Payment Channels,” arXiv preprint, 2018. [Online]. Available: https://arxiv.org/abs/1811.12740.
- [22]Z. Avarikioti, L. Heimbach, Y. Wang, and R. Wattenhofer, “Ride the Lightning: The Game Theory of Payment Channels,” in FC, 2020, pp. 264–283.
- [23]G. Avarikioti, R. Scheuner, and R. Wattenhofer, “Payment Networks as Creation Games,” in CBT, 2019, pp. 195–210.
- [24]O. Ersoy, S. Roos, and Z. Erkin, “How to Profit from Payments Channels,” in FC, 2020, pp. 284–303.
- [25]C. Badertscher, J. Garay, U. Maurer, D. Tschudi, and V. Zikas, “But why does it Work? A Rational Protocol Design Treatment of Bitcoin,” in Eurocrypt, 2018, pp. 34–65.
- [26]I. Eyal and E. G. Sirer, “Majority is not Enough: Bitcoin Mining is Vulnerable,” in FC, 2014, pp. 436–454.
- [27]Y. Kwon, D. Kim, Y. Son, E. Vasserman, and Y. Kim, “Be Selfish and avoid Dilemmas: Fork after Withholding (faw) Attacks on Bitcoin,” in CCS, 2017, pp. 195–209.
- [28]A. Sapirshtein, Y. Sompolinsky, and A. Zohar, “Optimal Selfish Mining Strategies in Bitcoin,” in FC, 2016, pp. 515–532.
- [29]A. Kiayias, E. Koutsoupias, M. Kyropoulou, and Y. Tselekounis, “Blockchain Mining Games,” in EC, 2016, pp. 365–382.
- [30]X. Chen, C. Papadimitriou, and T. Roughgarden, “An Axiomatic Approach to Block Rewards,” in AFT, 2019, pp. 124–131.
- [31]I. Eyal, “The Miner's Dilemma,” in IEEE S&P, 2015, pp. 89–103.
- [32]J. Teutsch, S. Jain, and P. Saxena, “When Cryptocurrencies Mine their own Business,” in FC, 2016, pp. 499–514.
- [33]E. Heilman, A. Kendler, A. Zohar, and S. Goldberg, “Eclipse Attacks on Bitcoin's Peer-to-Peer Network,” in {USENIX} Security, 2015, pp. 129–144.
- [34]K. Nayak, S. Kumar, A. Miller, and E. Shi, “Stubborn Mining: Generalizing Selfish Mining and Combining with an Eclipse Attack,” in EuroS&P, 2016, pp. 305–320.
- [35]Z. Liu, C. Nguyen, W. Wang, D. Niyato, P. Wang, Y.-C. Liang, and D. I. Kim, “A Survey on Blockchain: A Game Theoretical Perspective,” IEEE Access, pp. 47615–47643, 2019.
- [36]K. Chatterjee, A. K. Goharshady, and Y. Velner, “Quantitative Analysis of Smart Contracts,” in ESOP, 2018, pp. 739–767.
- [37]K. Chatterjee, A. Goharshady, and A. Pourdamghani, “Probabilistic Smart Contracts: Secure Randomness on the Blockchain,” in ICBC, 2019, pp. 403–412.
- [38]G. Malavolta, P. Moreno-Sanchez, A. Kate, M. Maffei, and S. Ravi, “Concurrency and Privacy with Payment-Channel Networks,” in CCS, 2017, p. 455–471.
- [39]S. Rain, Z. Avarikioti, L. Kovács, and M. Maffei, “Towards a Game- Theoretic Security Analysis of Off-Chain Protocols,” CoRR, vol. abs/2109.07429, 2021. [Online]. Available: https://arxiv.0rg/abs/2109.07429.
- [40]S. Mazumdar, P. Banerjee, A. Sinha, S. Ruj, and B. Roy, “Strategic Analysis to Defend against Griefing Attack in Lightning Network,” 2022. [Online]. Available: https://arxiv.org/abs/2203.10533.
- [41]P. Banerjee, S. Mazumdar, and S. Ruj, “Griefing-Penalty: Countermeasure for Griefing Attack in Bitcoin-compatible PCNs,” CoRR, vol. abs/2005.09327, 2020. [Online]. Available: https://arxiv.org/abs/2005.09327.
- [42]M. J. Osborne, Introduction to Game Theory. Oxford University PressUSA, 2004.
- [43]R. Mckelvey, A. McLennan, and T. Turocy, “Gambit: Software Tools for Game Theory,” 2005.
- [44]R. Savani and B. Von Stengel, “Game Theory Explorer - Software for the Applied Game Theorist,” CoRR, vol. abs/1403.3969, 2014.
- [45]O. Goldreich and Y. Oren, “Definitions and Properties of Zero-Knowledge Proof Systems,” J. of Cryptology, vol. 7, no. 1, pp. 1–32, 1994.

