Virtual Battery Models for Load Flexibility from Commercial Buildings

1.   Introduction

The deep penetration of renewable energy resources and the massive integration of intelligent communication and control devices is transforming the structure and functionality of electric power systems. One of the challenges in integrating renewable-based generation resources, and the corresponding decrease in conventional generation, is the increased need for frequency regulation ^[1]. Instantaneous imbalance between power supply and demand causes the system frequency to deviate from its nominal value. This deviation must be kept to a minimum for proper operation of many devices. Generators provide frequency regulation by adjusting their generation according to a signal sent from the system operator. Loads can also provide this service by adjusting their consumption as needed. Furthermore, many loads can modify their consumption more quickly than conventional generators, which makes them ideal for providing this service.

Within the context above, many recent papers have focused on the use of small residential loads with the ability to store thermal energy ^[2]–^[5]; we call these thermostatically controller loads (TCLs) because they incorporate a thermostat that simply switches them on and off based on measured temperature. Commercial buildings are another load with the ability to store thermal energy and the flexibility to provide frequency regulation ^[6]. The HVAC systems of these buildings typically have a much larger control input space. For example, through the use of dampers or variable frequency drives, air flow and power consumption can be continuously varied within some limits. The fact that these buildings can be quite large in terms of both power consumption and thermal mass, combined with the ability to continuously vary the power consumption, could eliminate the need to aggregate them with other similar loads; this simplifies the communication and control with remote devices, although the local control to be implemented is more complex.

In order for a building to provide regulation, it must have a controller which can utilize the flexibility of the load to follow a regulation signal. To this end, we design a controller, the sole function of which is to do this while respecting occupant comfort constraints and equipment ratings. We note that the HVAC control system design may have other objectives, such as total energy cost minimization ^[7]. A natural extension of our proposed controller would balance minimizing energy costs with maximizing income from the regulation market to minimize total costs.

Beyond designing the controller described above, in this paper we are interested in quantifying the flexibility of commercial buildings. Flexibility is defined as acceptable perturbations to baseline power, which is the power the building would have consumed were it not providing the regulation service. The details of flexibility and baseline power would be calculated based on the rules of the relevant electricity markets. Our tool for quantifying flexibility of loads is the virtual battery, which is a simple, succinct, and well understood model. The authors of ^[2] demonstrate the power of this model to describe the aggregate flexibility of a collection of TCLs. In this paper, we show that the virtual battery model has the power to capture the flexibility of more complex loads, and provide a method to identify its parameters.

Our proposed method for identifying the parameters of the virtual battery model requires a detailed model of the building being studied and its HVAC control system. We use this model to perform software-based tests to determine equivalent battery parameters; these tests stress the system by issuing carefully selected commands to the controller. By noting which commands cause the controller to fail and at what time, our method can deduce how the real system will react to certain inputs; this is useful to determine how much frequency regulation can be offered in the market.

There is a small amount of literature in which techniques related to ours have been suggested. For example, in ^[8], charge rate limits and capacity parameters are identified for a collection of TCLs; our proposed method improves upon this technique in two ways. First, we identify the parameters in terms of a more accurate model that includes dissipation. Second, we do not rely on the ability to command a load to consume a maximum or minimum possible power. Although this may be simple for a collection of TCLs, it is not clear this can be done for more complicated systems.

The remainder of the paper is organized as follows. In Section 2 we introduce the model of the HVAC test system used in all the case studies, and formulate our proposed controller. In Section 3 we will formulate the problem of identifying the parameters of the virtual battery model describing the flexibility of the HVAC system. In Section 4 we present the algorithms we will use to solve the identification problem. Section 5 presents the results of our procedure on the test system. Concluding remarks are presented in Section 6.

2.   Dynamic Model and Control

In this section, we introduce the HVAC model of the system used in this work and formulate a controller that enables the use of this system for frequency regulation.

2.1. HVAC System Model

In order to describe the behavior of the building HVAC system, we will adapt a variable air volume with reheat model; the formulation is borrowed from ^[7]. We will not include heating coils in the formulation as they are typically powered by gas. If these coils were being utilized, no electric power would be consumed, thus the overall electric power usage could not be reduced. Also, electric power consumption could be increased by turning on the AC, but this would be wasteful from an energy perspective.

Let $T_{z}$ denote the vector of building zone temperatures, and let $\dot{m}_{z}$ denote the vector of mass flow rates of cooled air into each zone. Also, let $d_{r}$ denote the fraction of return air that is recycled into the system, and let $T_{c}$ be the cooling coil outlet air temperature. Additionally let $\dot{Q}_{\text{offset}}$ be the vector of thermal loads independent of zone temperatures. Then, the dynamics of the system can be described by $$\begin{align*} M\frac{d}{dt}T_{z}(t)=&RT_{z}(t)+\dot{Q}_{\text{offset}}(t)\\ &+c_{p}\dot{m}_{z}(t).^{*}(1\!\!1 T_{c}(t)-T_{z}(t)), {\tag{1}} \end{align*}$$ where $1\!\!1=[1,\ \ldots,\ 1]^{T},.^{*}$ denotes an elementwise product, $M$ is a diagonal matrix of thermal capacitances associated with each building zone, $R$ is a matrix of thermal resistances associated with each building zone, and $c_{p}$ is the specific heat capacity of air.

Additional variables relate the dynamics in (1) to the electric power consumed by the HVAC system. Specifically, the electric power consumed by the supply fan, $P_{f}$, is given by $$\begin{equation*} P_{f}(t)=\kappa_{f}(1\!\!1^{T}\dot{m}_{z}(t))^{2}, {\tag{2}} \end{equation*}$$ and the electric power consumed by the cooling coils, $P_{c}$, is given by $$\begin{equation*} P_{c}(t)=\frac{c_{p}}{\eta_{h}}1\!\!1^{T}\dot{m}_{z}(t)(T_{m}(t)-T_{c}(t)), {\tag{3}} \end{equation*}$$ where $T_{m}$ is the cooling coil inlet air temperature which is given by $$\begin{equation*} T_{m}(t)=(1-d_{r}(t))T_{oa}(t)+d_{r}(t)T_{r}(t), \end{equation*}$$ where $T_{r}$ is the average return air temperature, which can be obtained as follows: $$\begin{equation*} T_{r}(t)=\frac{\dot{m}_{z}(t)^{T}T_{z}(t)}{1\!\!1^{T}\dot{m}_{z}(t)}. \end{equation*}$$ Finally, we need to consider the constraints which arise from acceptable occupant comfort: $$\begin{equation*} \underline{T}_{z}\leq T_{z}(t)\leq\overline{T}_{z},\ \ 0\leq d_{r}(t)\leq\overline{d}_{r}, {\tag{4}} \end{equation*}$$ as well as those that arise from the ratings of the equipment: $$\begin{equation*} \underline{\dot{m}}_{z}\leq\dot{m}_{z}(t)\leq\overline{\dot{m}}_{z},\ \ \underline{T}_{c}\leq T_{c}(t)\leq T_{m}. {\tag{5}} \end{equation*}$$

In the remainder, we will assume that $d_{r}=1$ and $T_{c} < \min(\underline{T}_{zi})$, where $\underline{T}_{zi}$ is the $i^{th}$ entry of the vector $\underline{T}_{zi}$. These assumptions are not a requirement for any future development, but they result in a cleaner formulation which is better for illustration purposes. The state vector $T_{z}$ remains unchanged. Also, we will define the control input, $s(t)$, as a function of flow rates as follows: $s(t)=c_{p}\dot{m}_{z}(t).^{*}(T_{c}1\!\!1[-T_{z}(t))$. Finally, we will neglect inter-zonal energy transfer. The matrix $R$ becomes a diagonal matrix proportional to the difference between ambient and zonal temperatures, and $\dot{Q}_{\text{offset}}$ is a vector of thermal loads that are independent of both ambient and zone temperatures. With these simplifications, the dynamic model in (1) becomes $$\begin{equation*} M \frac{d}{dt}T_{z}(t)=R(T_{oa}1\!\!1-T_{z}(t))+\dot{Q}_{\text{offset}}+s(t). {\tag{6}} \end{equation*}$$

The expression for the fan power in (2) becomes $$\begin{equation*} P_{f}(t)=\frac{\kappa_{f}}{c_{p}}(1\!\!1^{T}(s(t)./(T_{C}1\!\!1-T_{z}(t))))^{2}, {\tag{7}} \end{equation*}$$ where ./ denotes an elementwise division, and the expression for the cooling coil power in (3) becomes $$\begin{equation*} P_{c}(t)=-1\!\!1^{T}\frac{s(t)}{\eta_{h}}. {\tag{8}} \end{equation*}$$

The constraints in (4) – (5) result in $$\begin{align*} \underline{T}_{z}&\leq T_{z}(t)\leq\overline{T}_{z},{\tag{9}}\\ \underline{s}(t)&\leq s(t)\leq\overline{s}(t). {\tag{10}} \end{align*}$$

2.2. Baseline Power

We define the regulation power at time $t$ as the difference between the actual power consumed by the fan and cooling coils, i.e., $P_{f}(t)+P_{c}(t)$, and some baseline power, denoted by $P^{0}$, which is the total electric power consumed by the system were it not providing the regulation services. In this paper, we consider $P^{0}$ to be the value obtained from the steady state solution of (6), with the zone temperatures set to their midpoint values $T_{z}^{\text{m}}=\frac{1}{2}(\underline{T}_{z}+\overline{T}_{z})$. In subsequent developments, we will assume this solution satisfies (9) and (10). Thus, by setting the left hand side of (6) to zero, it immediately follows that $$\begin{equation*} s^{0}=-(RT_{z}^{\text{m}}+\dot{Q}_{\text{offset}}). {\tag{11}} \end{equation*}$$

From (11), we can calculate the baseline power using (7) and (8), which results in $$\begin{equation*} P^{0}=-1\!\!1 ^{T}\frac{s^{0}}{\eta_{h}}+\frac{\kappa_{f}}{c_{p}}(1\!\!1^{T}(s^{0}./(T_{c}1\!\!1-T_{z}^{\text{m}})))^{2}.\end{equation*}$$

2.3. Controller Design

Previous work on TCLs have proposed various controllers including a priority stack scheme ^[2]. Such a design is not applicable to this system because we have continuous control inputs rather than a number of binary ones, thus we propose a new controller which is appropriate for more general systems.

The controller's input is a commanded power output, $P^{*}$, which is equal to the desired regulation plus the baseline power. The output is a control, $s(t), t > 0$, which causes the HVAC system to consume the requested amount of power while also respecting the limits in (9) and (10). First, we check for feasibility, and if there exists an input, $s(t), t > 0$, such that all constraints are satisfied, we choose to optimize $s(t), t >0$, so temperatures are driven towards their midpoints. We can pose this problem as a nonlinear least square error estimation problem: $$\begin{equation*}\begin{matrix} s^{*}(t)=\arg\min_{s(t)} &\Vert T_{z}(t+\Delta t)-T_{z}^{\text{m}}\Vert_{2}\hfill\\ \text{subject to} &\underline{T}_{z}\leq T_{z}(t+\Delta t)\leq\overline{T}_{z}\hfill\\ &\underline{s}(t)\leq s(t)\leq\overline{s}(t)\hfill\\ &P^{*}(t)-P_{f}(t)-P_{c}(t)=0.\hfill\end{matrix}{\tag{12}}\end{equation*}$$

If there is no feasible solution to (12), the controller degrades gracefully by finding an alternative solution that minimizes the error without violating state or input constraints. The optimization problem then becomes: $$\begin{equation*} \begin{matrix}s^{*}(t)=\arg\min_{s(t)}&\vert P^{*}(t)-P_{f}(t)-P_{c}(t)\vert\hfill\\ \text{subject to} &\underline{T}_{z}\leq T_{z}(t+\Delta t)\leq\overline{T}_{z}\hfill\\ &\underline{s}(t)\leq s(t)\leq\overline{s}(t).\hfill\end{matrix} {\tag{13}} \end{equation*}$$

This behavior is not required for the parameter identification algorithm proposed in Section 4, but it would be desirable when implementing the controller in a real system.

3.   Virtual Battery Parameter Estimation

We first propose a function which performs software-based stress tests to determine which regulation signals the HVAC system is capable of following. Then, we introduce a reduced order model—the virtual battery model—that we will use to describe the more complex system. Using these, we formulate a criterion for the quality of the virtual battery model for describing the behavior of the full nonlinear HVAC system model. The problem is then to find the parameters that optimize this criterion.

3.1. Violation Time Function

We define a scalar input $u(t)=P^{*}(t)-P^{0}$ which represents the commanded deviation from the baseline power consumption profile. If a constraint is violated, we will assume the behavior of the system is undefined.

Assume we are free to choose $u(t)$, but have no knowledge of the structure or parameters of the underlying system and cannot make measurements beyond checking if constraints have been violated. For concreteness, assume that we have a function $f(u(t),\ T)$ which applies the input $u(t)$ to the system and, if there is a constraint violation at or before $t=T$, stops and returns the time $t_{v}$ at which a constraint was violated, otherwise it returns $\infty$. In other words: $$\begin{equation*} f(u(t), T)=\begin{cases} \infty &\text{if}\ \exists\ \text{solution to}\ (12)\ \forall t\leq T\hfill\\ t_{v} &\text{otherwise}\hfill \end{cases}{\tag{14}}\end{equation*}$$ where $t_{v}=\min t$ such that there is no solution to (12).

3.2. Virtual Battery Model

We believe the flexibility of many buildings can be accurately modeled by a virtual battery model; the dynamics of this battery model are given by: $$\begin{equation*} \dot{x}(t)=-ax(t)-u(t), {\tag{15}} \end{equation*}$$ where $x(t)\in \mathbb{R}, u(t)\in \mathbb{R}$, and $a > 0$ is a constant. There are upper and lower bounds constraining $x(t)$ and $u(t)$, i.e., $$\begin{equation*} -C\leq x(t)\leq C,\ \ -\underline{n}\leq u(t)\leq\overline{n}, {\tag{16}} \end{equation*}$$ where $C > 0, \underline{n} > 0, \overline{n} > 0$ are constant. If a constraint is violated, the behavior is undefined. We group the parameters into a vector $\phi=[a,C,\overline{n},\underline{n}]^{T}$ to make notation more compact.

Let $b(u(t), \phi,T)$ be a function which applies the input $u(t)$ to the battery model in (15) and, if a constraint in (16) is violated before time T, returns the time $t_{v}$ at which a constraint was violated, otherwise it returns $\infty$. Thus, similar to (17), we have that $$\begin{equation*} b(u(t),\phi, T)=\begin{cases} \infty &\text{if}\ (15)\ -(16)\ \text{hold}\ \forall r\leq T\hfill\\ t_{v} &\text{otherwise}\hfill\end{cases}{\tag{17}}\end{equation*}$$ where $t_{v}=\min t$ such that (15) – (16) are not satisfied.

3.3. Problem Statement

We want to find the values of the virtual battery model parameters in (15) and (16), which will allow us to predict the behavior of the dynamic model in (6) – (10) and (12) – (13). The quality of the fit is inversely related to the difference between the violation times predicted by the nonlinear system and those predicted by the virtual battery model. If the fit is not exact, we wish to err on the side of caution by constraining the battery model to predict a violation sooner than would occur in the nonlinear model. This ensures that if an input does not cause a violation on the identified battery model, it will not not cause a violation in the nonlinear model. Mathematically, the problem can be formulated as finding a set of parameters $\phi^{*}$ such that $$\begin{equation*} \begin{matrix}\phi^{*}=\arg\min_{\phi} &\Vert b(u(t),\phi,T)-f(u(t),\ T)\Vert\hfill\\ \text{subject to} &b(u(t),\phi, T)\leq f(u(t),\ T),\hfill \end{matrix}{\tag{18}} \end{equation*}$$ for all values of $u(t)$.

Figure 1.Figure 1. System identification setup.

4.   Estimation Algorithms

In this section we will propose algorithms for identifying the parameters of the virtual battery model capturing the flexibility of the HVAC system as described by the dynamic model (6) – (10) and (12) – (13). The basic structure of the proposed identification setup is shown in Fig. 1, where $P^{*}$ is commanded power and $s$ is a vector of control signals. Feedback includes actual power $P$ and zone temperatures $T_{z}$.

4.1. Estimation of Rate Limits

The first step of the proposed procedure is to identify the rate limits $\overline{n}$ and $\underline{n}$. If the initial state is within its bounds and we apply an input and a constraint is immediately violated (i.e., $f(u(0),0)=\infty$), we know it was due to the input constraints; this is because some finite time is required for an input to affect the value of the state.

We know $\overline{n} > 0(\underline{n} > 0)$, but we do not know an upper bound. We therefore perform a one-sided binary search to find an upper bound. Once we have an upper bound, we use it together with the greatest lower bound in a binary search procedure to find $\overline{n}(\underline{n})$ to arbitrary precision $\varepsilon$; the details of this procedure for estimating $\overline{n}$ are laid out in Algorithm 1. The procedure for $\underline{n}$ is similar, but with $f(\cdot,0)$ replaced with $g(\cdot,0)=f(-\cdot,0)$.

Algorithm 1Algorithm 1   Rate limit search algorithm

4.2. Estimation of Capacity and Dissipation Constant

If we respect the previously identified rate limits, we can guarantee that any constraint violation error is due to the capacity limit. In general, dissipation cannot be neglected when solving for the capacity limit so the two must be solved for simultaneously.

Let $u(t)=k$ be constant and $x(0)=x_{0}$. The solution to (15) is given by $$\begin{equation*} x(t)=\left(x_{0}+\frac{k}{a}\right)e^{-at}-\frac{u}{a}. \end{equation*}$$ Then, by setting $x(t_{v})=-C, x_{0}=0$ and solving for $t_{v}$, we obtain that $$\begin{equation*} t_{v}=b(k,\phi, T)=-\frac{1}{a}\log\left(1+\frac{-aC}{k}\right), {\tag{19}} \end{equation*}$$ if $k > aC$.

Because we are trying to fit the behavior of a linear model to that of a nonlinear one, we must look for a sufficient solution instead of an exact one. We say a solution is sufficient in the sense that verifying that an input does not cause any violations in the virtual battery model is sufficient to guarantee that the same input will not cause violations in the full nonlinear model. We are unable to prove that a solution is sufficient, i.e., the constraint in (18) will hold for all $u(t)$, because of the nonlinearity in (7); instead, we propose a heuristic. In Section 5 we will provide empirical evidence for the effectiveness of this heuristic procedure.

We start the procedure by picking a large value of $T$ and generating $u_{1}(t), \ldots,u_{n}(t)$ such that violation times will be finite. Constant functions with different (log-distributed) magnitudes are a natural first choice, but others can be used. Then, we can construct a vector of violation times given by the nonlinear model: $F=[f(u_{1}(t),\ T),\ \ldots,f(u_{n}(t),\ T)]^{T}$. We also construct a vector of violation times given by the linear model: $B(a,C)=[b(u_{1}(t), \phi,T), \ldots,b(u_{n}(t), \phi,T)]^{T}$. The parameters $a$ and $C$ enter the calculation through the parameter vector $\phi$.

We wish the find the values of $a$ and $C$ so the two models have similar violation times. If the difference in times cannot be reduced to zero, we require that the violation time predicted by the virtual battery model be less than that of the nonlinear model. We can cast this problem as a constrained nonlinear least squares problem: $$\begin{equation*} \begin{matrix}\text{minimize}_{a,C} &\Vert B(a,C)-F\Vert_{2}\hfill\\ \text{subject to} &B(a,C)\leq F.\hfill\end{matrix} {\tag{20}} \end{equation*}$$

If $u(t), t\geq 0$, is constant, we can write an analytic expression for $b$ as in (19), but in general we cannot analytically solve for the first $t_{v}$ at which the equality given by $$\begin{equation*} x(t_{v})=-\int_{0}^{t_{v}}e^{-a(t_{v}-\tau)}u(\tau)d\tau=\pm C {\tag{21}} \end{equation*}$$ holds; this occurs for all but the simplest $u(t), t\geq 0$. If this is the case, we can use a numerical method within the function $b$, just like we must use for $f$. Given $x(0)=0, \,\dot{x}(t)=-ax(t)-u(t)$ we can approximate the system trajectory, $x(t), t > 0$, until $\vert x(t_{v})\vert =C$, and record $t_{v}$. This change makes the computation of $B$ to take orders of magnitude longer, but we found that solving (20) is still computationally tractable. Because $f$ needs to be calculated only once, we expect the procedure to scale well to large systems.

5.   Numerical Estimation Results

We begin this section by examining the behavior of the controller and building/HVAC system model presented in Section 2. We will then test the performance of the identification procedure described in Section 4 on the aforementioned system. These studies use the system parameters in Table 1.

5.1. Controller Performance Verification

In the first study, we examine the behavior of the controller proposed in Section 2 and verify its functionality. The baseline power is calculated to be 4.17kW. Fig. 2 shows that initial zonal temperatures are evenly distributed through the acceptable range indicated by dashed lines. We see that the controller initially drives temperatures toward the midpoints, as desired. Minimum flow rate constraints are initially binding for zones 1 through 4. The commanded power is then stepped from 0 kW to 1 kW. The controller initially issues commands that perfectly meet the request. Temperatures decrease until temperature constraints become binding. At this point the controller is unable to meet the requested power, so there is a positive error.

5.2. Charge Rate Limit Estimation

We next use the estimation procedure outlined in Section 4 to identify the positive charge rate limits $\overline{n}$ and $\underline{n}$. We obtain that $\overline{n}=103.7\text{kW}$ and $\underline{n}=2.44\text{kW}$; the asymmetry is quite large because, for the chosen parameters, the air conditioning system is capable of blowing much more cold air than required to maintain a steady temperature. On the other hand, the baseline air flow is quite close to the lower limit, so it cannot consume much less than the baseline power value. For this reason, this system would be much better utilized in a market that treats up and down regulation as two distinct services.

5.3. Capacity and Dissipation Estimation

The next step is to identify capacity and dissipation parameters. For this task, a set of test inputs needs to be chosen. We investigate a number of different families of inputs and compare their performance. The parameters identified using the different techniques are remarkably consistent; the results are summarized in Table 2.

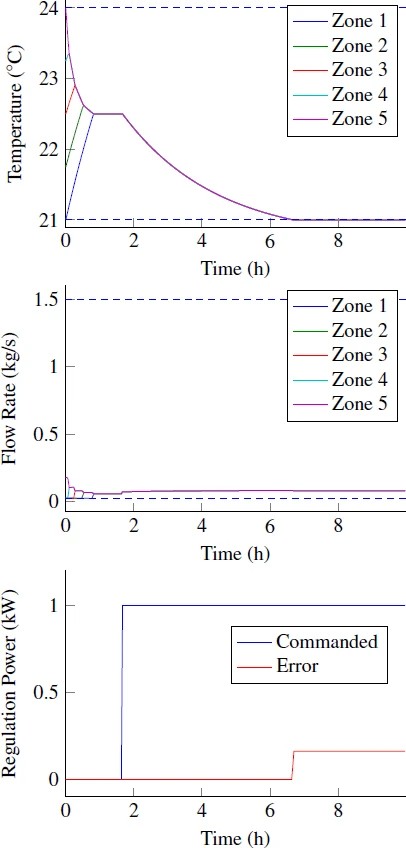
Figure 2.Figure 2. Response to step regulation signal.

5.3.1. Step Input

We first test the use of inputs of the form $u(t)=k, t\geq 0$, with $k\in \mathbb{R}$. Fifty values of $k$ were chosen logarithmically distributed between a value just above $ac$ (which can be found using a search procedure similar to the one outlined in Algorithm 1) up to $\overline{n}$. Fig. 3 provides a plot of violation time versus input magnitude. If $a=0$, we would expect a straight line with slope −1. The line curves upward for small inputs because there is more time for the effects of the dissipation to manifest themselves.

Step inputs are simple enough that we can find an analytic solution to (21); thus we have a choice of calculating $b$ using an analytic expression or a numerical solver. In this regard, the optimization procedure in (20) runs orders of magnitude faster with the analytic expression, and the identified parameters were confirmed to be nearly identical in either case.

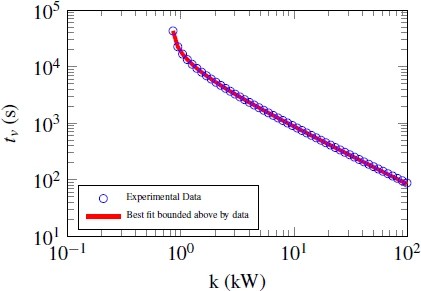
Figure 3.Figure 3. Best battery model bounded above by constant input experimental data.

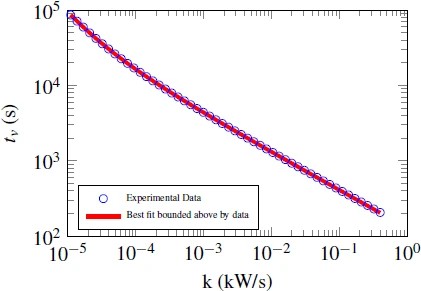
Figure 4.Figure 4. Best battery model bounded above by ramp input experimental data.

5.3.2. Ramp Input

Fig. 4 shows the result for inputs of the form $u(t)=kt, t\geq 0$, with $k\in \mathbb{R}$. Again, we calculate the parameters using both an analytic expression, which is given by $$\begin{equation*} t_{v}=\frac{1}{a}\left(1+\frac{a^{2}C}{k}+W(-e^{-1-\frac{a^{2}C}{k}})\right), \end{equation*}$$ where $W$ is the Lambert $W$ function ^[9], and a numerical solver; both approaches yield identical results. The identified parameters also agree with those identified using the step inputs.

5.3.3. RC Step Input

Fig. 5 shows the result for inputs of the form $u(t)=k(1-e^{-\lambda t}), t\geq 0$, with $k\in \mathbb{R}$, and $\lambda=5\times 10^{-5}\text{s}^{-1}$. For a given $k$, violation times with this input are larger than the instantaneous step input because $u(0)=0$ and $u(t)$ approaches $k$ asymptotically. For this type of input and the following types, there is not an analytical expression for the violation time, so we only test the numerical methods. In the end, the identified parameters agree with the previous values identified using step functions.

Figure 5.Figure 5. Best battery model bounded above by RC charging step input.

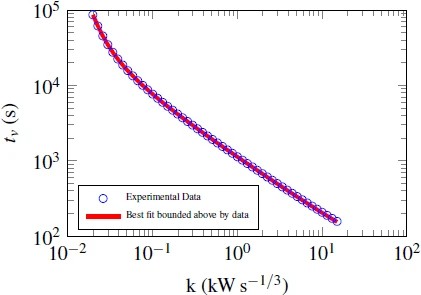
Figure 6.Figure 6. Best battery model bounded above by monomial.

5.3.4. Monomial Input

Fig. 6 shows the result for inputs of the form $u(t)=kt^{\lambda}, t\geq 0$, with $k\in \mathbb{R}$, and $\lambda=\frac{1}{3}$. The parameters obtained using this input provide further evidence for the consistency of the results among different input types.

5.3.5. Regulation Signal Step Input

Fig. 7 shows violation time vs input constant using a modified regulation signal $u(t)=r(t)(k(r(t) > 0)+\underline{n}(r(t) < 0))$, where $r(t)$ is the PJM dynamic regulation signal from ^[10]. A representative segment of this signal is shown in Fig. 8. This asymmetric signal was selected because of the asymmetric nature of the charge rate constraints. A symmetric signal that respects $\underline{n}$ would never violate a capacity limit and would not provide limited economic benefit. Providing asymmetric regulation is possible in markets such as CAISO, where up regulation and down regulation are treated as different services.

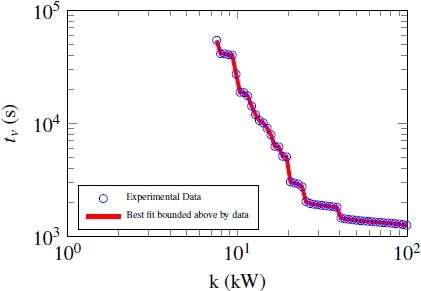
Figure 7.Figure 7. Best battery model identified by regulation signal.

Of all the tests, this had the most issues with convergence, step sizes, and tolerances. This is likely due to the input function not being monotonic. With a monotonic function, a small integration or interpolation error will lead to a small change in violation time. This is not the case with this input signal. A small difference (for example, the nonlinear data uses Euler's method, but the battery model uses Runge-Kutta) can lead to a much bigger difference in violation time. Even with this difficulty, the estimated parameters using this input match those obtained with the other aforementioned approaches (see Table 2). Conversely, the parameters identified using the other inputs performed practically identically in predicting violation times from the regulation signal. Overall this is excellent empirical evidence to support our proposed stress-based estimation procedure for this system.

Figure 8.Figure 8. Portion of modified dynamic regulation input signal, $k=99.5$.

6.   Concluding Remarks

We have introduced a controller which allows for the HVAC system of a commercial building to provide frequency regulation and demonstrated its behavior. We have introduced a method whereby the ability of the resulting closed-loop system to provide frequency can be sufficiently modeled as a simple, well understood battery model. Although the estimation method is an approximation, it was found to perform remarkably accurately on our test system.

There are a number of issues we are planning to further develop in our future work. First, we believe the proposed identification technique is quite general; thus, we plan to test the performance of our procedure on additional types of systems, including those the exact dynamics of which are unknown, but may be inferred from historical data. Another issue worth exploring is relaxing the assumption that all parameters, including ambient air temperature and acceptable comfort temperature ranges, are constant in time. Further research could examine how time varying system parameters affect battery parameters. Additionally, we could test how quickly the identification procedure can detect these changes. Finally, in our procedure, we initialize our system with zero initial charge. If this were not the case, we would likely want to determine up and down capacities separately. The current charge would be difference from the midpoint of the up and down capacities.